Задания по теме «Прикладные задачи»
Открытый банк заданий по теме прикладные задачи. Задания B10 из ЕГЭ по математике (профильный уровень)
Открытый банк заданий по теме прикладные задачи. Задания B10 из ЕГЭ по математике (профильный уровень)
Скорость колеблющегося на пружине груза меняется по закону v=4\sin\pi t (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения груза превышала 2 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Заметим, что в течение первой секунды, то есть при 0\leqslant t\leqslant1 выполняется неравенство 0\leqslant\pi t\leqslant\pi. Из этого неравенства следует, что: \sin\pi t\geqslant0.
Тогда 4\sin\pi t\geqslant2,
\sin\pi t\geqslant\frac12,
\frac{\pi}{6}\leqslant\pi t\leqslant\frac{5\pi}{6} (см. рис.),
\frac16\leqslant t\leqslant\frac56.
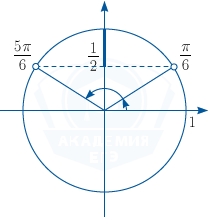
Значит, на первой секунде скорость движения превышала 2 см/с на протяжении \frac56-\frac16=\frac23\approx 0,67 секунды.
После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и вычисляет расстояние до воды по формуле h=5t^2, где h — расстояние в метрах, t — время падения в секундах. Время падения камешков до дождя составляло 0,4 с. Определите, насколько должен подняться уровень воды в колодце после дождя, чтобы измеряемое время изменилось на 0,1 с? Ответ выразите в метрах.
Пусть h_0 — расстояние до воды до дождя, h — после дождя (в метрах). После дождя время падения t уменьшится и станет равно 0,4-0,1=0,3 с. Тогда h_0-h= 5(t_0^2-t^2)= 5(0,4^2-0,3^2)= 0,35.
Груз массой 0,4 кг колеблется на пружине. Его скорость меняется по закону v=v_0\cos\frac{2\pi t}{T}, где t — время с момента начала колебаний, T=2 с — период колебаний, v_0=0,3 м/с. Кинетическая энергия E груза измеряется в джоулях и определяется формулой E=\frac{mv^2}{2}, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 3 секунды после начала колебаний. Ответ дайте в джоулях.
E=\frac{m\left(v_0\cos\dfrac{2\pi t}{T}\right)^2}{2},
E=\frac{0,4\left(0,3\cos\dfrac{2\pi\cdot3}{2}\right)^2}{2}= 0,2\cdot0,09= 0,018.
Кинетическая энергия груза через 3 секунды после начала колебаний равна 0,018 Дж.
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m=6 кг и радиусом R=12 см и двух боковых с массами M=2 кг и радиусами R+h. Момент инерции катушки относительно своей оси вращения, определяется формулой I=\frac{(m+2M)R^2}{2}+M(2Rh+h^2) и выражается в кг · см2. Определите, при каком наибольшем значении h момент инерции катушки не превышает предельного значения 770 кг · см2? Ответ выразите в сантиметрах.
Решим неравенство I\leqslant770 относительно h, учитывая, что m=6, R=12, M=2.
\frac{(6+2\cdot2)\cdot12^2}{2}\,+ 2(2\cdot12h+h^2)\leqslant770,
720+48h+2h^2\leqslant770,
h^2+24h-25\leqslant0,
откуда -25\leqslant h\leqslant1.
Максимальное значение h равно 1 сантиметру.
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a км/ч2. Скорость v определяется формулой v=\sqrt{2la}, где l — пройденный автомобилем путь. С каким ускорением должен двигаться автомобиль, чтобы, преодолев расстояние 0,7 километра, он приобрел бы скорость 98 км/ч. Ответ выразите в км/ч2.
v=\sqrt{2la}, v^2=2la, a=\frac{v^2}{2l}.
Подставляем в эту формулу l=0,7, v=98:
Получаем: a=\frac{98^2}{2\cdot0,7}=6860.
Итак, ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,7 километра, приобрести скорость 98 км/ч, равно 6860 км/ч2.
Автомобиль, масса которого равна m=1100 кг, начинает двигаться с ускорением, которое в течение t секунд остаётся неизменным, и за это время преодолевает расстояние S = 600 метров. Сила (в ньютонах), приложенная к автомобилю в это время, равна F=\frac{2mS}{t^2}. Найдите наибольшее время за которое автомобиль преодолеет указанный путь после начала движения, если известно, что сила F, приложенная к нему, не меньше 3300 H. Ответ выразите в секундах.
Решим неравенство F\geqslant3300.
\frac{2mS}{t^2}\geqslant3300,
\frac{2\cdot1100\cdot600}{t^2}\geqslant 3300,
\frac{2\cdot100\cdot2}{t^2}\geqslant 1.
t^2\leqslant 400,
-20\leqslant t\leqslant 20.
Наибольшее время после начала движения автомобиля, за которое он пройдёт 600 метров, равно 20 секундам.
Автомобиль, движущийся в начальный момент времени со скоростью v_0 = 12 м/с, начал торможение с постоянным ускорением a = 4 м/с2. После начала торможения за t секунд автомобиль преодолел расстояние S=v_0t-\frac{at^2}{2} (м). Сколько секунд прошло с момента начала торможения, если за это время автомобиль проехал 16 метров?
Подставим данные задачи в формулу S=v_0t-\frac{at^2}{2}.
16=12t-\frac{4t^2}{2},
t^2-6t+8=0,
t_1=4,\,t^2=2.
С помощью формулы скорости при равнозамедленном движении v=v_0-at найдём время движения автомобиля до остановки: v=0, v_0=12 м/с, a=4 м/с2; 0=12-4t, откуда t=3. Итак, автомобиль остановится через 3 секунды после начала торможения.
Учитывая, что t\leqslant3, получим, что от момента начала торможения прошло 2 секунды.
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна I=\frac{\varepsilon}{R+r}, где \varepsilon — ЭДС источника (в вольтах), r = 2 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 40% от силы тока короткого замыкания Iкз = \frac{\varepsilon}{r}? Ответ выразите в омах.
Решим неравенство I\leqslant0,4\cdot Iкз при условии, что r=2 Ом.
\frac{\varepsilon}{R+r}\leqslant0,4\cdot\frac{\varepsilon}{r},
\frac{1}{R+2}\leqslant\frac{4}{10\cdot2},
\frac{1}{R+2}\leqslant\frac15,
R\geqslant3.
Итак, наименьшее сопротивление цепи, при котором сила тока будет составлять не более 40% от силы тока короткого замыкания, равно 3 Ом.
Перед отправкой тепловоз издал гудок с частотой f_0 = 280 Гц. Чуть позже гудок издал подъезжающий к платформе тепловоз. В следствие движения тепловоза, частота второго гудка оказалась больше первого (эффект Доплера). Она зависит от скорости источника сигнала по закону: f(v)=\frac{f_0}{1-\dfrac vc} (Гц), где c — скорость звука (в м/с). Сигналист, стоящий на платформе, следит за движением тепловоза и успешно распознает сигналы, если они отличаются не менее чем на 7 Гц. Найдите наименьшую скорость приближающегося к платформе тепловоза, если сигналист смог различить издаваемые сигналы, а скорость звука равна 328 м/с. Ответ выразите в м/с.
Решим неравенство f(v)-f_0\geqslant7, используя условие v<328.
\frac{f_0}{1-\dfrac vc}-f_0\geqslant7,
\frac{280}{1-\dfrac{v}{328}}-280\geqslant7,
\frac{1}{1-\dfrac{v}{328}}-1\geqslant\frac{1}{40},
\frac{1}{1-\dfrac{v}{328}}\geqslant\frac{41}{40},
1-\frac{v}{328}\leqslant\frac{40}{41},
\frac{v}{328}\geqslant\frac{1}{41},
v\geqslant8.
Следовательно, минимальная скорость тепловоза равна 8 м/с.
Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1+8t-5t^2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее четырёх метров?
Решим относительно t неравенство h(t)\geqslant4.
-5t^2+8t+1\geqslant4,
5t^2-8t-1\leqslant-4,
5t^2-8t+3\leqslant0.
Найдем корни уравнения 5t^2-8t+3=0:
Вычислим дискриминант: D=b^2-4ac= -8^2-4\cdot5\cdot3= 64-60=4,
t_{1,2}= \frac{-b\pm\sqrt D}{2a}= \frac{8\pm\sqrt4}{2\cdot5}= \frac{8\pm2}{10},
t_1=\frac35,\,t_2=1;
5\left ( t-\frac35 \right ) \left ( t-1 \right )\leqslant0, откуда \frac35\leqslant t\leqslant1. Мяч будет находиться на высоте не мене четырех метров в течение 1-\frac35=\frac25=0,4 секунды.
Закажите обратный звонок!