Задания по теме «Квадратные и степенные уравнения»

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и вычисляет расстояние до воды по формуле h=5t^2, где h — расстояние в метрах, t — время падения в секундах. Время падения камешков до дождя составляло 0,4 с. Определите, насколько должен подняться уровень воды в колодце после дождя, чтобы измеряемое время изменилось на 0,1 с? Ответ выразите в метрах.

Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m=6 кг и радиусом R=12 см и двух боковых с массами M=2 кг и радиусами R+h. Момент инерции катушки относительно своей оси вращения, определяется формулой I=\frac{(m+2M)R^2}{2}+M(2Rh+h^2) и выражается в кг · см². Определите, при каком наибольшем значении h момент инерции катушки не превышает предельного значения 770 кг · см²? Ответ выразите в сантиметрах.

Автомобиль, движущийся в начальный момент времени со скоростью v_0 = 12 м/с, начал торможение с постоянным ускорением a = 4 м/с². После начала торможения за t секунд автомобиль преодолел расстояние S=v_0t-\frac{at^2}{2} (м). Сколько секунд прошло с момента начала торможения, если за это время автомобиль проехал 16 метров?

Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1+8t-5t^2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее четырёх метров?

По боковой стенке промышленного цилиндрического бака у самого дна закреплен кран. После открытия крана вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону H(t)=H_0-kt\sqrt{2gH_0}+\frac{g}{2}k^2t^2, где

H_0=45 м — начальный уровень воды;

t — время в секундах, прошедшее с момента открытия крана;

k=\frac{1}{50} — отношение площадей поперечных сечений крана и бака;

g = 10 м/с² — ускорение свободного падения.

К какому моменту времени высота столба воды в баке составит не более 20 м? Ответ выразите в секундах.

Месячный доход r некоторого предприятия на рынке определяется формулой r(p)=q\cdot p (тыс. руб.), где:

q — объем спроса на продукцию;

p — цена.

Причем объем спроса зависит от цены по формуле: q=300-60p.

Определите при каком максимальном уровне цены на продукцию p (тыс. руб.) предприятие получит доход не менее 315 тыс. руб. в месяц.

Некоторый прибор может безопасно нагреваться до температуры 1750 К, после чего срабатывает термопредохранитель, отключающий его. Экспериментальным путем был получен закон, по которому нагревается прибор в течение непрерывной работы: 

T(t)=at^2 + bt + T_0, где:

T(t) – температура прибора (К);

T₀ = 1450 К;

t – время работы прибора (мин);

b = 175 К/мин;

\alpha = -12,5 К/мин².

Определите наибольшее время, которое способен проработать прибор. Ответ выразите в минутах.

Одним из знаменитейших мостов в мире считается мост «Золотые Ворота» в Сан-Франциско. Вы и сами наверняка видели его в американских фильмах. Сконструирован он следующим образом: между двумя огромными пилонами, установленными на берегу, протянуты основные несущие цепи, к которым, перпендикулярно земле, вертикально подвешиваются балки. К этим балкам, в свою очередь, крепится полотно моста. При большой протяженности моста применяются дополнительные опоры. В этом случае висячий мост состоит из «сегментов».

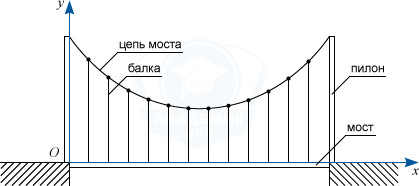
На рисунке изображена схема одного из сегментов моста. Обозначим начало координат в точке установки пилона, ось Ox направим по полотну моста, а Oy – вертикально вдоль пилона. Расстояние от пилона до балок и между балками составляет 100 метров.

Определите длину ближайшей к пилону балки, если форма цепи моста определяется уравнением:

y=0,0061\cdot x^2-0,854\cdot x+33

в котором x и y – величины, которые измеряются в метрах. Ответ выразите числом в метрах.