Задание №1092
Условие
Скорость колеблющегося на пружине груза меняется по закону v=4\sin\pi t (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения груза превышала 2 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Решение
Заметим, что в течение первой секунды, то есть при 0\leqslant t\leqslant1 выполняется неравенство 0\leqslant\pi t\leqslant\pi. Из этого неравенства следует, что: \sin\pi t\geqslant0.
Тогда 4\sin\pi t\geqslant2,
\sin\pi t\geqslant\frac12,
\frac{\pi}{6}\leqslant\pi t\leqslant\frac{5\pi}{6} (см. рис.),
\frac16\leqslant t\leqslant\frac56.
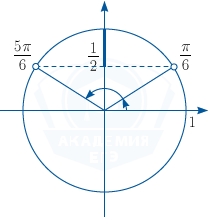
Значит, на первой секунде скорость движения превышала 2 см/с на протяжении \frac56-\frac16=\frac23\approx 0,67 секунды.
Ответ
0,67
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Полина Малина /