Открытый банк заданий по теме тригонометрические уравнения. Задания B10 из ЕГЭ по математике (профильный уровень)
Скорость колеблющегося на пружине груза меняется по закону v=4\sin\pi t (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения груза превышала 2 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Заметим, что в течение первой секунды, то есть при 0\leqslant t\leqslant1 выполняется неравенство 0\leqslant\pi t\leqslant\pi. Из этого неравенства следует, что: \sin\pi t\geqslant0.
Тогда 4\sin\pi t\geqslant2,
\sin\pi t\geqslant\frac12,
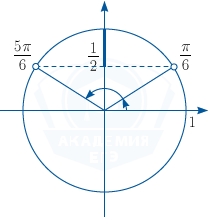
\frac{\pi}{6}\leqslant\pi t\leqslant\frac{5\pi}{6} (см. рис.),
\frac16\leqslant t\leqslant\frac56.
Значит, на первой секунде скорость движения превышала 2 см/с на протяжении \frac56-\frac16=\frac23\approx 0,67 секунды.
Груз массой 0,4 кг колеблется на пружине. Его скорость меняется по закону v=v_0\cos\frac{2\pi t}{T}, где t — время с момента начала колебаний, T=2 с — период колебаний, v_0=0,3 м/с. Кинетическая энергия E груза измеряется в джоулях и определяется формулой E=\frac{mv^2}{2}, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 3 секунды после начала колебаний. Ответ дайте в джоулях.
E=\frac{m\left(v_0\cos\dfrac{2\pi t}{T}\right)^2}{2},
E=\frac{0,4\left(0,3\cos\dfrac{2\pi\cdot3}{2}\right)^2}{2}= 0,2\cdot0,09= 0,018.
Кинетическая энергия груза через 3 секунды после начала колебаний равна 0,018 Дж.
Небольшой мячик бросают под острым углом \alpha к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле L=\frac{v_0^2}{g}\sin2\alpha(м), где
v_0=15 м/с — начальная скорость мячика,
g — ускорение свободного падения (считайте g = 10 м/с2).
Определите минимальный угол броска мячика, при котором он сможет перелететь реку шириной 11,25 м. Ответ дайте в градусах.
Решим неравенство L\geqslant11,25.
\frac{v_0^2}{g}\sin2\alpha\geqslant\frac{45}{4},
\frac{15^2}{10}\sin2\alpha\geqslant\frac{45}{4},
\frac12\sin2\alpha\geqslant\frac14,
\sin2\alpha\geqslant\frac12.
Так как \alpha — острый угол, то 0<\alpha<\frac{\pi}{2},
0<2\alpha<\pi, тогда
\frac{\pi}{6}\leqslant2\alpha\leqslant\frac{5\pi}{6},
2\alpha\geqslant\frac{\pi}{6},
\alpha\geqslant\frac{\pi}{12}=15^{\circ}.
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который в последствии переводится в электрический сигнал, изменяющийся со временем по закону U=U_0\cos(\omega t+\varphi), где t - время (с), U_0 = 30 B — амплитуда сигнала, частота \omega=80^{\circ}/c, фаза \varphi=30^{\circ}. На датчике установлена лампочка, которая горит в случае, если напряжение в нем не ниже чем 15 B. Определите, какую часть времени в процентах в первую секунду времени работы датчика будет гореть лампочка.
По условию U=30\cos(80^{\circ}t+30^{\circ}). Лампочка горит, если U\geq15, то есть \cos(80^{\circ}t+30^{\circ})\geq0,5.
Рассмотрим промежуток времени t\in[0; 1].
При этом 80^{\circ}t+30^{\circ} меняется от 30^{\circ} до 110^{\circ}, при этом \cos(80^{\circ}t+30^{\circ})\geq0,5, если аргумент меняется от 30^{\circ} до 60^{\circ}.
Лампочка будет гореть \frac{30}{80} первой секунды, или \frac{30}{80}\cdot100=37,5%.
Небольшой мяч бросили к горизонту с начальной скоростью 26 м/с под углом \alpha. Максимальную высоту полёта мяча H можно найти по формуле:
H=\frac{v_{0}^{2}}{4g}\cdot (1-\cos{2\alpha }), при этом:
H – максимальная высота (м);
v0 – начальная скорость мяча (м/с);
g = 10 м/с2 – ускорение свободного падения;
\alpha – угол между вектором броска и поверхностью земли.
Найдите значение угла \alpha, под которым был брошен мяч, если известно, что при максимальной высоте полета мяч находился над препятствием высотой 7,45 на расстоянии 1 м. Ответ укажите в градусах.
Выразим косинус двойного угла из условия задачи:
H=\frac{v_{0}^{2}}{4g}\cdot (1-\cos{2\alpha })
1-\cos{2\alpha} = \frac{H\cdot 4g }{v_{0}^{2}}
\cos{2\alpha} = 1 - \frac{4Hg }{v_{0}^{2}}
Подставим числовые значения в выражение:
\cos{2\alpha} = 1 - \frac{4\cdot (7,45+1)\cdot 10 }{26^2}
\cos{2\alpha} = 1 - \frac{4\cdot 8,45\cdot 10 }{26\cdot 26}= 1 - \frac{1}{2}=\frac{1}{2}
2\alpha=60 ^{\circ} \Rightarrow \alpha=30 ^{\circ} – угол, под которым был брошен мяч.
Закажите обратный звонок!