Задания по теме «Задачи на доказательство»
Открытый банк заданий по теме задачи на доказательство. Задания C4 из ЕГЭ по математике (профильный уровень)
Открытый банк заданий по теме задачи на доказательство. Задания C4 из ЕГЭ по математике (профильный уровень)
В трапеции KLMN боковая сторона KL перпендикулярна основаниям. Из точки K на сторону MN опустили перпендикуляр KA. На стороне KL отмечена точка B так, что прямые LA и BN параллельны.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите отношение LA:BN, если угол LMN равен 150^{\circ}.
а) Для доказательства перпендикулярности прямых BM и MN достаточно доказать, что BM \parallel KA, а это выполняется в случае, если подобны треугольники SBM и SKA, то есть если справедливо равенство \frac{SB}{SK}=\frac{SM}{SA}.
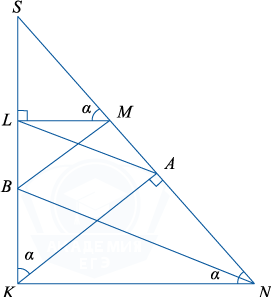
Пусть \angle SML=\alpha , тогда \angle SKA=\angle ANK=\alpha. Из параллельности прямых LA и BN следует, что треугольники SLA и SBN подобны, значит, верно равенство \frac{SL}{SB}=\frac{SA}{SN}.
В прямоугольном треугольнике SLM, \frac{SL}{SM}=\sin \alpha , откуда SM =\frac{SL}{\sin \alpha }.
В прямоугольном треугольнике SAK, \frac{SA}{SK}=\sin \alpha ,
В прямоугольном треугольнике SKN, \frac{SK}{SN}=\sin \alpha. SK=SN \sin \alpha.
Перемножая почленно равенства \frac{SA}{SK}=\sin \alpha и \frac{SK}{SN}=\sin \alpha , получим: \frac{SA}{SN}=\sin ^2 \alpha , SA=SN \sin ^2 \alpha. Учитывая, что \frac{SA}{SN}=\frac{SL}{SB}, имеем \frac{SL}{SB}=\sin ^2 \alpha , откуда SB =\frac{SL}{\sin ^2 \alpha }.
Тогда \frac{SB}{SK}= \frac{SL}{\sin ^2 \alpha\cdot SN\cdot \sin \alpha }= \frac{SL}{\sin ^3 \alpha\cdot SN}.
\frac{SM}{SA}= \frac{SL}{\sin \alpha\cdot SN \sin ^2 \alpha }= \frac{SL}{\sin ^3 \alpha\cdot SN}. Правые части равенств равны, следовательно, \frac{SB}{SK}=\frac{SM}{SA}, значит, прямые LA и BN параллельны, и BM и MN перпендикулярны.
б) В силу подобия треугольников SML и SKN, \frac{LA}{BN}=\frac{SL}{SB}.
Как показано в пункте а), \frac{SL}{SB}=\sin ^2 \alpha. По условию \angle LMN=150^{\circ}, \angle LMN+\alpha =180^{\circ}, \alpha =180^{\circ}-150^{\circ}=30^{\circ}.
\frac{SL}{SB}=\sin ^2 \alpha =\sin ^2 30^{\circ}=\frac14.
б) \frac14.
Две окружности, с центрами O_{1} и O_{2} соответственно касаются внешним образом. Из точки O_{1} проведена касательная O_{1}K ко второй окружности (K — точка касания), а из точки O_{2} проведена касательная O_{2}L к первой окружности (L — точка касания), точки касания K и L лежат по разные стороны от прямой O_{1}O_{2}.
а) Докажите, что \angle O_{1}KL=\angle O_{1}O_{2}L.
б) Найдите радиус меньшей окружности, если дополнительно известно, что он в 4 раза меньше радиуса большей окружности, а площадь четырёхугольника O_{1}KO_{2}L равна 54+9\sqrt{6}.
а) По свойству касательной к окружности O_{1}L \perp O_{2}L и O_{1}K \perp O_{2}K. Прямоугольный \bigtriangleup O_{1}O_{2}K вписан в некоторую окружность с диаметром O_{1}O_{2}.
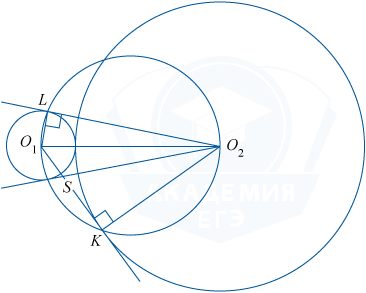
Аналогично прямоугольный \bigtriangleup O_{1}O_{2}L вписан в некоторую окружность с тем же диаметром. Следовательно, \bigtriangleup O_{1}O_{2}K и O_{1}O_{2}L вписаны в одну и ту же окружность, то есть точки O_{1}, O_{2}, K, L лежат на окружности с диаметром O_{1}O_{2}. Значит, \angle O_{1}O_{2}L и \angle O_{1}KL — вписанные и опираются на одну и ту же дугу O_{1}L. Отсюда, \angle O_{1}KL=\angle O_{1}O_{2}L.
б) Пусть O_{1}L — радиус меньшей окружности. Обозначим его через r. Следовательно, O_{2}K=4r. Тогда O_{1}O_{2}=r+4r=5r. Отсюда из \bigtriangleup O_{1}LO_{2} по теореме Пифагора O_{2}L=\sqrt{(5r)^2-r^2}=2\sqrt{6}r. Из \bigtriangleup O_{1}KO_{2} по теореме Пифагора O_{1}K=\sqrt{(5r)^2-(4r)^2}=3r.
S_{O_{1}LO_{2}}=\frac{1}{2}O_{1}L \cdot LO_{2}=\sqrt{6}r^2.
S_{O_{1}KO_{2}}=\frac{1}{2}O_{2}K \cdot O_{1}K=6r^2.
S_{O_{1}KO_{2}L}= S_{O_{1}LO_{2}}+S_{O_{1}KO_{2}}= (6+\sqrt{6})r^2.
Из условия следует, что S_{O_{1}KO_{2}L}=54+9\sqrt{6}. Тогда (6+\sqrt{6})r^2=54+9\sqrt{6}, (6+\sqrt{6})r^2=9(6+\sqrt{6}), r=3.
3
В прямоугольнике ABCD AB=24, AD=23. К окружности, радиус которой равен 12, с центром в точке A из точки C проведена касательная, которая пересекает сторону AD в точке M.
а) Докажите, что CM=2AM.
б) Найдите длину отрезка AM.
а) Используя условие задачи, выполним рисунок.
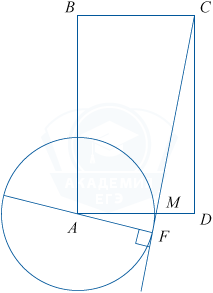
Проведём радиус AF в точку касания. AF \perp CF. \bigtriangleup AFM \sim \bigtriangleup MCD по двум углам (\angle AFM=\angle CDM=90^\circ, \angle AMF=\angle CMD как вертикальные).
AF:CD=12:24=1:2, откуда следует, что AM:MC=1:2, то есть MC=2AM.
б) Пусть AM=x, тогда CM=2x, MD=23-x. Для прямоугольного треугольника CDM справедлива теорема Пифагора:
CM^2=CD^2+MD^2, т.е. 4x^2=24^2+(23-x)^2,
3x^2+46x-1105=0.
Решая квадратное уравнение, получим x=13. Итак, AM=13.
13
ABCD — прямоугольник. Окружность с центром в точке A радиуса AD пересекает продолжение стороны DA в точке K. Прямая KB пересекает прямую CD в точке P, а окружность во второй раз — в точке M.
а) Докажите, что CP=CM.
б) Найдите BD, если AM=15, MC=8.
а) Докажем, что DM \perp PK и CD=CP, а затем воспользуемся свойством медианы CM прямоугольного треугольника DPM. ABCD — прямоугольник, поэтому его углы прямые и CB=AD, CD=AB. \angle PCB=\angle BAK=90^\circ.
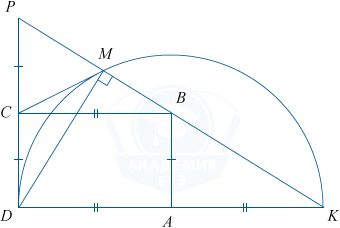
AD=AK как радиусы окружности. Получаем, что CB=AK. \angle PBC=\angle BKA как соответственные углы при CB \parallel AD (секущая PK).
\bigtriangleup PBC=\bigtriangleup BKA (по стороне и двум прилежащим к ней углам), значит, AB=CP. Но CD=AB, из этого получаем CD=CP.
\angle DMK — вписанный, он опирается на диаметр, значит, \angle DMK=90^\circ.
\angle PMD=180^\circ-\angle DMK=90^\circ. В прямоугольном треугольнике PDM медиана CM равна половине гипотенузы PD, значит, MC=CP=CD.
б) Воспользуемся теоремой Пифагора для треугольника BAD. BD^{2}=AD^{2}+AB^{2} (по теореме Пифагора). AM=AD (радиусы), AD=15. MC=CD=8 (см. пункт а). BD=\sqrt{15^{2}+8^{2}}=17.
17
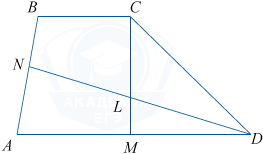
В трапеции ABCD точка M — середина основания AD, точка N выбрана на стороне AB так, что площадь четырёхугольника ANLM равна площади треугольника CLD, где L — точка пересечения отрезков CM и DN.
а) Докажите, что N — середина стороны AB.
б) Найдите, какую часть от площади трапеции ABCD составляет площадь четырёхугольника ANLM, если BC=4, AD=6.
а) По условию S_{ANLM}=S_{CLD}, следовательно, S_{ANLM}+S_{LMD}=S_{CLD}+S_{LMD}, S_{ANLM}+S_{LMD}=S_{AND}.
S_{CLD}+S_{LMD}=S_{CMD}, значит, S_{AND}=S_{CMD}.
2S_{AND}=2S_{CMD}=S_{ACD}=S_{ABD} (треугольники ACD и ABD имеют общее основание AD и общую высоту).
Итак, 2S_{AND}=S_{ABD}=S_{AND}+S_{BND}, откуда следует, что S_{AND}=S_{BND}, а это означает, что точка N — середина стороны AB (у треугольников AND и BND общая высота). Что и требовалось доказать.
б) Пусть K — точка пересечения прямых CN и AD. \bigtriangleup AKN=\bigtriangleup BCN (по стороне и двум прилежащим углам). Поэтому S_{ABCD}=S_{CKD}.
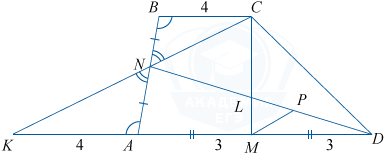
Проведем MP \parallel KC, тогда из подобия треугольников \bigtriangleup NCL и \bigtriangleup LMP (\angle MLP =\angle NLC, \angle LPM=\angle CNL) \frac{CL}{LM}=\frac{CN}{MP}=\frac{KN}{MP}.
Из подобия треугольников \bigtriangleup KND и \bigtriangleup DMP (KN \parallel MP)
\frac{KN}{MP}=\frac{KD}{MD}=\frac{10}{3}. Значит, \frac{CL}{LM}=\frac{KN}{MP}=\frac{10}{3}; \frac{CL}{CM-CL}=\frac{10}{3};
3CL=10CM-10CL, 13CL=10CM, следовательно,
\frac{CL}{CM}=\frac{10}{13}=\frac{S_{CLD}}{S_{CMD}}, откуда S_{CLD}=\frac{10}{13}S_{CMD}.
\frac{S_{CMD}}{S_{CKD}}=\frac{MD}{KD}=\frac{3}{10}, откуда S_{CMD}=\frac{3}{10}S_{CKD}=\frac{3}{10}S_{ABCD}.
Подставляя S_{CMD}=\frac{3}{10}S_{ABCD} в равенство S_{CLD}=\frac{10}{13}S_{CMD},
получим S_{CLD}= \frac{10}{13}S_{CMD}= \frac{10}{13} \cdot \frac{3}{10}S_{ABCD}= \frac{3}{13}S_{ABCD}. Учитывая, что S_{ANLM}=S_{CLD}, окончательно получим S_{ANLM}=\frac{3}{13}S_{ABCD}.
\frac{3}{13}
В трапеции ABCD, в которой AD \parallel BC, точка M — точка пересечения боковых сторон AB и CD. Прямая MN пересекает основания AD и BC в точках P и Q соответственно. Точка N является точкой пересечения диагоналей трапеции.
а) Докажите, что AP=PD и BQ=QC.
б) Найдите отношение \frac{BC}{AD}, если \frac{BD}{BN}=\frac{7}{5}.
а) Проведём EK \parallel BC \parallel AD через точку N.
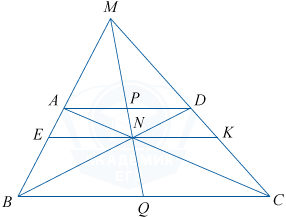
1. \bigtriangleup AND \sim \bigtriangleup BNC (по двум углам): \angle BCN = \angle CAD, \angle CBN = \angle NDA. Отсюда, \frac{BN}{ND}=\frac{NC}{AN}.
Тогда \frac{BN}{ND}+1=\frac{NC}{AN}+1, то есть \frac{BN+ND}{ND}=\frac{NC+AN}{AN}, \frac{BD}{ND}=\frac{AC}{AN} (1)
2. \bigtriangleup ABC \sim \bigtriangleup AEN \Rightarrow \frac{BC}{EN}=\frac{AC}{AN} (2)
Аналогично \bigtriangleup BCD \sim \bigtriangleup NKD \Rightarrow \frac{BC}{NK}=\frac{BD}{ND}. С учетом (1) получим \frac{BC}{NK}=\frac{AC}{AN}. Из последнего равенства, с учётом (2), получим \frac{BC}{NK}=\frac{BC}{EN}. Отсюда, NK=EN (3)
3. \bigtriangleup APM \sim \bigtriangleup ENM (по двум углам) \Rightarrow \frac{AP}{EN}=\frac{MP}{NM}.
Аналогично \frac{PD}{NK}=\frac{MP}{NM}. Следовательно, \frac{AP}{EN}=\frac{PD}{NK}.
4. С учётом (3), получим AP=PD, что и требовалось доказать.
Аналогично \frac{EN}{BQ}=\frac{MN}{MQ}=\frac{NK}{QC}\Rightarrow BQ=QC, что и требовалось доказать.
б) \frac{BC}{AD}=\frac{BN}{ND}=\frac{BN}{BD-BN};
\frac{AD}{BC}= \frac{BD-BN}{BN}= \frac{BD}{BN}-1= \frac{7}{5}-1= \frac{2}{5}. Значит, \frac{BC}{AD}=\frac{5}{2}.
\frac{5}{2}
Вневписанная окружность с центром O_a и радиусом r_a в прямоугольном \bigtriangleup ABC касается в точке T_a катета BC. А вневписанная окружность с центром O_b касается катета AC в точке T_b.
а) Докажите, что площадь прямоугольного треугольника ABC может быть получена использованием формулы S = r_ar_b.
б) Зная S_{ABC}=30, найдите площадь четырехугольника AT_bT_aB.
а) Обозначим AB=c, \: AC=b, \: CB=a, p — полупериметр \bigtriangleup ABC.
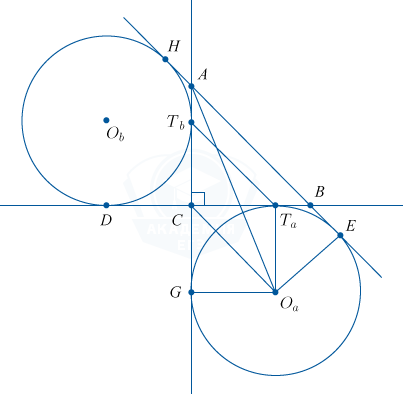
Выполняются следующие равенства:
S=S_{ABC}=S_{O_{a}CA}+S_{O_{a}BA}-S_{O_{a}CB}=
=\frac{1}{2}O_{a}G \cdot AC+\frac{1}{2}O_{a}E \cdot AB-\frac{1}{2}O_{a}T_{a} \cdot BC=
=\frac{1}{2}r_{a}b+\frac{1}{2}r_{a}c-\frac{1}{2}r_{a}a=\frac{r_{a}}{2}(c+b-a).
Отсюда получаем r_{a}=\frac{2S}{c+b-a}. Аналогично получается формула r_{b}=\frac{2S}{c+a-b}.
Используя формулы r_{a}=\frac{2S}{c+b-a}, r_{b}=\frac{2S}{c+a-b}, c^{2}=a^{2}+b^{2} и S=\frac{ab}{2}, получаем:
r_{a}r_{b}= \frac{4S^{2}}{(b+c-a)(a+c-b)}= \frac{4S^{2}}{c^{2}-(b-a)^{2}}= \frac{4S^{2}}{2ab}= \frac{2S^{2}}{2S}= S, то есть S= r_{a}r_{b}.
б) Так как S_{ABC}=r_{a}r_{b} и площадь прямоугольного треугольника T_{a}CT_{b} равна \frac{1}{2} \cdot CT_{a} \cdot CT_{b}=\frac{1}{2} \cdot r_{a}r_{b}=15, то искомая площадь равна 30-15=15.
15
Высоты BQ и AH проведены из вершин A и B тупоугольного треугольника ABC. BH=BQ; \: BH:BC=1:3; \angle B — тупой.
а) Докажите, что диаметр окружности, описанной вокруг треугольника ABQ в \sqrt{3} раз больше BQ.
б) Площадь треугольника HQC равна 16. Найдите площадь четырехугольника AHBQ.
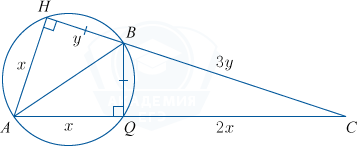
а) \bigtriangleup ABH=\bigtriangleup AQB по катету и гипотенузе (BH=BQ по условию, AB общая), следовательно, AH=AQ и \angle HAB=\angle BAQ. AB — биссектриса угла A в \bigtriangleup AHC , по свойству биссектрисы AH:AC=BH:BC=1:3. Обозначим AH=x, BH=y, тогда BC=3y, AQ=x, AC=3x, QC=2x.
По теореме Пифагора в \bigtriangleup BQC выполняется BQ^{2}+QC^{2}=BC^{2}, y^{2}+(2x)^{2}=(3y)^{2}, 4x^{2}=8y^{2}, x=\sqrt{2y}.
В прямоугольном \bigtriangleup ABQ AB^{2}=x^{2}+y^{2}=2y^{2}+y^{2}=3y^{2}, AB=\sqrt{3}y. Так как \bigtriangleup ABQ прямоугольный, то AB является диаметром описанной около него окружности. Мы получили, что диаметр описанной окружности \bigtriangleup ABQ=\sqrt{3}BQ.
б) S_{BQC}=\frac{1}{2}BQ \cdot QC=\frac{1}{2}y \cdot 2x=xy.
S_{AHBQ}=2S_{AHB}=2 \cdot \frac{1}{2} \cdot xy=xy, \: значит, S_{AHBQ}=S_{BQC}.
S_{HQC}=\frac{1}{2}HC \cdot QC \cdot \sin C,
S_{BQC}=\frac{1}{2}BC \cdot QC \cdot \sin C, \: тогда \frac{S_{HQC}}{S_{BQC}}=\frac {HC}{BC}=\frac{4y}{3y}=\frac{4}{3},
S_{HQC}=\frac{4}{3}S_{BQC}=\frac{4}{3}xy=16, \: xy=12.
S_{AHBQ}=2S_{ABQ}=2 \cdot\frac{1}{2} \cdot xy=xy=12.
12
Две произвольные окружности, касающиеся друг друга, вписаны в заданный угол, величиной \alpha, не превосходящей \pi.
а) Докажите, что отношение модуля разности радиусов к сумме радиусов этих окружностей является постоянной величиной.
б) Найдите радиус меньшей окружности, если угол \alpha=\frac{\pi}{3} и радиус большей окружности равен 10.
а) Обозначим заданный угол через ABC, радиусы окружностей r_{1} и r_{2} (r_{1}<r_{2}), а центры окружностей через O_{1} и O_{2} соответственно.
Так как центры окружностей равноудалены от сторон угла, то они лежат на биссектрисе угла B. Проведем из центров окружностей радиусы O_{1}T и O_{2}E в точки касания со стороной AB.
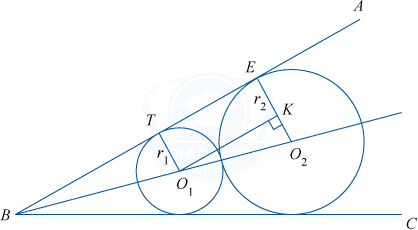
Тогда O_{1}T и O_{2}E перпендикулярны AB.
Из центра O_{1} меньшей окружности опустим перпендикуляр O_{1}K на радиус O_{2}E большей окружности. Получим прямоугольник O_{1}TEK. Тогда EK=TO_{1}=r_{1}. Следовательно, O_{2}K=O_{2}E-KE=r_{2}-r_{1}.
Так как O_{1}K \parallel AB, то \angle ABO_{2}=\angle KO_{1}O_{2}. Отметим также, что O_{2}O_{1}=r_{2}+r_{1}.
Отсюда следует, что \frac{r_{2}-r_{1}}{r_{2}+r_{1}}= \frac{O_{2}K}{O_{2}O_{1}}= \sin \angle KO_{1}O_{2}= \sin \angle ABO_{2}.
Но \angle ABO_{2}=\frac{\alpha}{2}, где \alpha — заданный угол, поэтому \frac{r_{2}-r_{1}}{r_{2}+r_{1}}=\sin \frac{\alpha}{2}.
б) Подставляя заданные значения \alpha и r_{2} в полученную выше формулу, получаем:
\frac{10-r_{1}}{10+r_{1}}=\sin \frac{\pi}{6}=\frac{1}{2}, 5+\frac{1}{2}r_{1}=10-r_{1}, \frac{3}{2}r_{1}=5, r_{1}=\frac{10}{3}.
\frac{10}{3}
Основание CD трапеции ABCD перпендикулярно ее боковой стороне BC. Через точки A и D провели окружность, которая касается прямой BC в точке M.
а) Докажите подобие \bigtriangleup ABF и \bigtriangleup FBK при условии, что F — точка пересечения прямых BC и AD, а BK — высота \bigtriangleup ABF.
б) При условии CD=4 см и AB=5 см, вычислите расстояние от точки M до прямой AD.
Не нарушая общности, можно рассмотреть одну из возможных конфигураций:
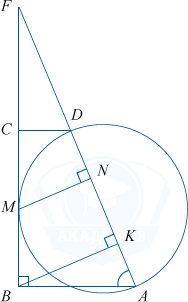
а) Высота \bigtriangleup ABF \: BK \perp AF \Rightarrow \bigtriangleup ABF и \bigtriangleup FBK — прямоугольные, они подобны (по общему углу F).
б) Проведем MN \perp AD. Тогда MN — расстояние от точки M до прямой AD.
\bigtriangleup ABF, \bigtriangleup MNF, \bigtriangleup CDF — прямоугольные, их острый угол F — общий, значит, они подобны.
\bigtriangleup MNF \sim \bigtriangleup ABF \Rightarrow \frac{MN}{AB}=\frac{FM}{FA}, MN=\frac{FM \cdot AB}{FA}.
\bigtriangleup MNF \sim \bigtriangleup DCF \Rightarrow \frac{MN}{CD}=\frac{FM}{FD}, MN=\frac{FM \cdot CD}{FD}.
Тогда получим MN^{2}= \frac{FM \cdot AB \cdot FM \cdot CD}{FA \cdot FD}= \frac{FM^{2} \cdot AB \cdot CD}{FA \cdot FD}.
По теореме о секущей и касательной имеем:
FM^{2}=AF \cdot FD, тогда MN^{2}=AB \cdot CD=20.
MN=\sqrt{20}=2\sqrt{5}.
2\sqrt{5}
Закажите обратный звонок!