Задание №222
Условие
Высоты BQ и AH проведены из вершин A и B тупоугольного треугольника ABC. BH=BQ; \: BH:BC=1:3; \angle B — тупой.
а) Докажите, что диаметр окружности, описанной вокруг треугольника ABQ в \sqrt{3} раз больше BQ.
б) Площадь треугольника HQC равна 16. Найдите площадь четырехугольника AHBQ.
Решение
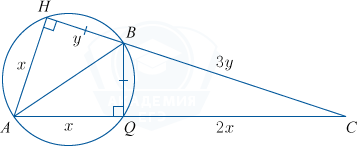
а) \bigtriangleup ABH=\bigtriangleup AQB по катету и гипотенузе (BH=BQ по условию, AB общая), следовательно, AH=AQ и \angle HAB=\angle BAQ. AB — биссектриса угла A в \bigtriangleup AHC , по свойству биссектрисы AH:AC=BH:BC=1:3. Обозначим AH=x, BH=y, тогда BC=3y, AQ=x, AC=3x, QC=2x.
По теореме Пифагора в \bigtriangleup BQC выполняется BQ^{2}+QC^{2}=BC^{2}, y^{2}+(2x)^{2}=(3y)^{2}, 4x^{2}=8y^{2}, x=\sqrt{2y}.
В прямоугольном \bigtriangleup ABQ AB^{2}=x^{2}+y^{2}=2y^{2}+y^{2}=3y^{2}, AB=\sqrt{3}y. Так как \bigtriangleup ABQ прямоугольный, то AB является диаметром описанной около него окружности. Мы получили, что диаметр описанной окружности \bigtriangleup ABQ=\sqrt{3}BQ.
б) S_{BQC}=\frac{1}{2}BQ \cdot QC=\frac{1}{2}y \cdot 2x=xy.
S_{AHBQ}=2S_{AHB}=2 \cdot \frac{1}{2} \cdot xy=xy, \: значит, S_{AHBQ}=S_{BQC}.
S_{HQC}=\frac{1}{2}HC \cdot QC \cdot \sin C,
S_{BQC}=\frac{1}{2}BC \cdot QC \cdot \sin C, \: тогда \frac{S_{HQC}}{S_{BQC}}=\frac {HC}{BC}=\frac{4y}{3y}=\frac{4}{3},
S_{HQC}=\frac{4}{3}S_{BQC}=\frac{4}{3}xy=16, \: xy=12.
S_{AHBQ}=2S_{ABQ}=2 \cdot\frac{1}{2} \cdot xy=xy=12.
Ответ
12