Задание №215
Условие
Две произвольные окружности, касающиеся друг друга, вписаны в заданный угол, величиной \alpha, не превосходящей \pi.
а) Докажите, что отношение модуля разности радиусов к сумме радиусов этих окружностей является постоянной величиной.
б) Найдите радиус меньшей окружности, если угол \alpha=\frac{\pi}{3} и радиус большей окружности равен 10.
Решение
а) Обозначим заданный угол через ABC, радиусы окружностей r_{1} и r_{2} (r_{1}<r_{2}), а центры окружностей через O_{1} и O_{2} соответственно.
Так как центры окружностей равноудалены от сторон угла, то они лежат на биссектрисе угла B. Проведем из центров окружностей радиусы O_{1}T и O_{2}E в точки касания со стороной AB.
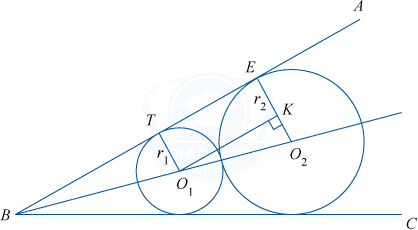
Тогда O_{1}T и O_{2}E перпендикулярны AB.
Из центра O_{1} меньшей окружности опустим перпендикуляр O_{1}K на радиус O_{2}E большей окружности. Получим прямоугольник O_{1}TEK. Тогда EK=TO_{1}=r_{1}. Следовательно, O_{2}K=O_{2}E-KE=r_{2}-r_{1}.
Так как O_{1}K \parallel AB, то \angle ABO_{2}=\angle KO_{1}O_{2}. Отметим также, что O_{2}O_{1}=r_{2}+r_{1}.
Отсюда следует, что \frac{r_{2}-r_{1}}{r_{2}+r_{1}}= \frac{O_{2}K}{O_{2}O_{1}}= \sin \angle KO_{1}O_{2}= \sin \angle ABO_{2}.
Но \angle ABO_{2}=\frac{\alpha}{2}, где \alpha — заданный угол, поэтому \frac{r_{2}-r_{1}}{r_{2}+r_{1}}=\sin \frac{\alpha}{2}.
б) Подставляя заданные значения \alpha и r_{2} в полученную выше формулу, получаем:
\frac{10-r_{1}}{10+r_{1}}=\sin \frac{\pi}{6}=\frac{1}{2}, 5+\frac{1}{2}r_{1}=10-r_{1}, \frac{3}{2}r_{1}=5, r_{1}=\frac{10}{3}.
Ответ
\frac{10}{3}