Задание №209
Условие
Основание CD трапеции ABCD перпендикулярно ее боковой стороне BC. Через точки A и D провели окружность, которая касается прямой BC в точке M.
а) Докажите подобие \bigtriangleup ABF и \bigtriangleup FBK при условии, что F — точка пересечения прямых BC и AD, а BK — высота \bigtriangleup ABF.
б) При условии CD=4 см и AB=5 см, вычислите расстояние от точки M до прямой AD.
Решение
Не нарушая общности, можно рассмотреть одну из возможных конфигураций:
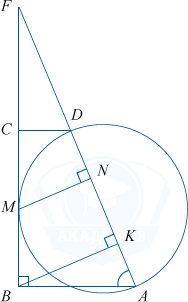
а) Высота \bigtriangleup ABF \: BK \perp AF \Rightarrow \bigtriangleup ABF и \bigtriangleup FBK — прямоугольные, они подобны (по общему углу F).
б) Проведем MN \perp AD. Тогда MN — расстояние от точки M до прямой AD.
\bigtriangleup ABF, \bigtriangleup MNF, \bigtriangleup CDF — прямоугольные, их острый угол F — общий, значит, они подобны.
\bigtriangleup MNF \sim \bigtriangleup ABF \Rightarrow \frac{MN}{AB}=\frac{FM}{FA}, MN=\frac{FM \cdot AB}{FA}.
\bigtriangleup MNF \sim \bigtriangleup DCF \Rightarrow \frac{MN}{CD}=\frac{FM}{FD}, MN=\frac{FM \cdot CD}{FD}.
Тогда получим MN^{2}= \frac{FM \cdot AB \cdot FM \cdot CD}{FA \cdot FD}= \frac{FM^{2} \cdot AB \cdot CD}{FA \cdot FD}.
По теореме о секущей и касательной имеем:
FM^{2}=AF \cdot FD, тогда MN^{2}=AB \cdot CD=20.
MN=\sqrt{20}=2\sqrt{5}.
Ответ
2\sqrt{5}