Задание №197
Условие
Точка O лежит за пределами квадрата ABCD, но в одной плоскости. OA=OB=5, OD=\sqrt{13}.
а) Докажите, что площадь квадрата ABCD меньше 36.
б) Найдите площадь квадрата ABCD.
Решение
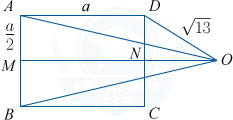
Точка O равноудалена от точек A и B, значит, лежит на срединном перпендикуляре к отрезку AB, то есть O принадлежит прямой MN.
а) Площадь квадрата не может быть больше либо равна 36, так как тогда сторона квадрата была бы больше либо равна 6, что невозможно. Действительно, в прямоугольном треугольнике катет всегда меньше гипотенузы, поэтому в прямоугольном треугольнике AOM верны соотношения MO=MN+NO<AO, откуда MN<AO, а так как MN=AB, то и AB<AO, AB \geqslant 6, AB<5=AO. Тогда 6<5, что неверно.
б) Введем обозначения AD=a, ON=x, тогда AM=MB=DN=\frac{a}{2}, MO=a+x. Применяя дважды теорему Пифагора для \bigtriangleup AMO и \bigtriangleup DNO, получим систему
\begin{cases}(a+x)^2+\frac{a^2}{4}=25,\\ x^2+\frac{a^2}{4}=13;\end{cases}
\begin{cases}a^2+2ax+x^2+\frac{a^2}{4}=25,\\ x^2+\frac{a^2}{4}=13;\end{cases}
\begin{cases}a^2+2ax-12=0,\\ x^2+\frac{a^2}{4}=13;\end{cases}
Из первого уравнения выразим x и подставим во второе:
x=\frac{12-a^2}{2a},
\left(\frac{12-a^2}{2a}\right)^2+\frac{a^2}{4}=13.
Выполняя тождественные преобразования, получим биквадратное уравнение a^4+38a^2+72=0, откуда a^2=36 или a^2=2.
Итак, площадь квадрата ABCD равна 2.
Ответ
2