Задание №229
Условие
Вневписанная окружность с центром O_a и радиусом r_a в прямоугольном \bigtriangleup ABC касается в точке T_a катета BC. А вневписанная окружность с центром O_b касается катета AC в точке T_b.
а) Докажите, что площадь прямоугольного треугольника ABC может быть получена использованием формулы S = r_ar_b.
б) Зная S_{ABC}=30, найдите площадь четырехугольника AT_bT_aB.
Решение
а) Обозначим AB=c, \: AC=b, \: CB=a, p — полупериметр \bigtriangleup ABC.
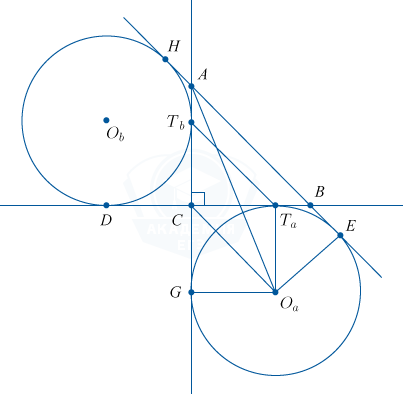
Выполняются следующие равенства:
S=S_{ABC}=S_{O_{a}CA}+S_{O_{a}BA}-S_{O_{a}CB}=
=\frac{1}{2}O_{a}G \cdot AC+\frac{1}{2}O_{a}E \cdot AB-\frac{1}{2}O_{a}T_{a} \cdot BC=
=\frac{1}{2}r_{a}b+\frac{1}{2}r_{a}c-\frac{1}{2}r_{a}a=\frac{r_{a}}{2}(c+b-a).
Отсюда получаем r_{a}=\frac{2S}{c+b-a}. Аналогично получается формула r_{b}=\frac{2S}{c+a-b}.
Используя формулы r_{a}=\frac{2S}{c+b-a}, r_{b}=\frac{2S}{c+a-b}, c^{2}=a^{2}+b^{2} и S=\frac{ab}{2}, получаем:
r_{a}r_{b}= \frac{4S^{2}}{(b+c-a)(a+c-b)}= \frac{4S^{2}}{c^{2}-(b-a)^{2}}= \frac{4S^{2}}{2ab}= \frac{2S^{2}}{2S}= S, то есть S= r_{a}r_{b}.
б) Так как S_{ABC}=r_{a}r_{b} и площадь прямоугольного треугольника T_{a}CT_{b} равна \frac{1}{2} \cdot CT_{a} \cdot CT_{b}=\frac{1}{2} \cdot r_{a}r_{b}=15, то искомая площадь равна 30-15=15.
Ответ
15