Задание №968
Условие
В трапеции ABCD, в которой AD \parallel BC, точка M — точка пересечения боковых сторон AB и CD. Прямая MN пересекает основания AD и BC в точках P и Q соответственно. Точка N является точкой пересечения диагоналей трапеции.
а) Докажите, что AP=PD и BQ=QC.
б) Найдите отношение \frac{BC}{AD}, если \frac{BD}{BN}=\frac{7}{5}.
Решение
а) Проведём EK \parallel BC \parallel AD через точку N.
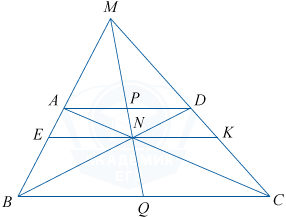
1. \bigtriangleup AND \sim \bigtriangleup BNC (по двум углам): \angle BCN = \angle CAD, \angle CBN = \angle NDA. Отсюда, \frac{BN}{ND}=\frac{NC}{AN}.
Тогда \frac{BN}{ND}+1=\frac{NC}{AN}+1, то есть \frac{BN+ND}{ND}=\frac{NC+AN}{AN}, \frac{BD}{ND}=\frac{AC}{AN} (1)
2. \bigtriangleup ABC \sim \bigtriangleup AEN \Rightarrow \frac{BC}{EN}=\frac{AC}{AN} (2)
Аналогично \bigtriangleup BCD \sim \bigtriangleup NKD \Rightarrow \frac{BC}{NK}=\frac{BD}{ND}. С учетом (1) получим \frac{BC}{NK}=\frac{AC}{AN}. Из последнего равенства, с учётом (2), получим \frac{BC}{NK}=\frac{BC}{EN}. Отсюда, NK=EN (3)
3. \bigtriangleup APM \sim \bigtriangleup ENM (по двум углам) \Rightarrow \frac{AP}{EN}=\frac{MP}{NM}.
Аналогично \frac{PD}{NK}=\frac{MP}{NM}. Следовательно, \frac{AP}{EN}=\frac{PD}{NK}.
4. С учётом (3), получим AP=PD, что и требовалось доказать.
Аналогично \frac{EN}{BQ}=\frac{MN}{MQ}=\frac{NK}{QC}\Rightarrow BQ=QC, что и требовалось доказать.
б) \frac{BC}{AD}=\frac{BN}{ND}=\frac{BN}{BD-BN};
\frac{AD}{BC}= \frac{BD-BN}{BN}= \frac{BD}{BN}-1= \frac{7}{5}-1= \frac{2}{5}. Значит, \frac{BC}{AD}=\frac{5}{2}.
Ответ
\frac{5}{2}