Задания по теме «Практические задачи»

1. Пусть x км/ч — скорость «быстрой» лодки, тогда (x-3) км/ч — скорость «медленной» лодки. Обозначим через t время движения лодок от начала движения до поворота (в часах).

2. Найдём время, затраченное «быстрой» лодкой на весь путь. Так как эта лодка сначала шла t часов против течения, то она прошла расстояние (x-2)\cdot t км. На обратный путь уже по течению она затратила время \frac{(x-2)t}{x+2} часов.

3 Аналогично, согласно условию, медленная лодка шла против течения t часов со скоростью ((x-3)-2)=(x-5) км/ч и прошла расстояние (x-5)\cdot t км. При этом x-5>0.

На обратный путь эта лодка затратила время \frac{(x-5)\cdot t}{(x-3)+2}=\frac{(x-5)\cdot t}{x-1} часов, так как шла по течению.

4. Согласно условию время движения «быстрой» лодки не менее, чем на \frac1{15} t больше времени движения «медленной» лодки. Поэтому справедливо неравенство

\frac{(x-2)t}{x+2}-\frac{(x-5)t}{x-1} \geqslant \frac1{15} t, (t>0),

\frac{x-2}{x+2}-\frac{x-5}{x-1}-\frac1{15} \geqslant 0, (x+2>0, x-1>0)

15(x-2)(x-1)-15(x-5)(x+2)\,\,- (x+2)(x-1) \geqslant 0,

15x^2-45x+30-15x^2+45x+150\,\,- x^2-x+2 \geqslant 0,

-x^2-x+182 \geqslant 0,

x^2+x-182 \leqslant 0.

Решаем неравенство графически. Находим корни трёхчлена x^2+x-182.

x_{1,2}= \frac{-1\pm \sqrt {1+4\cdot 182}}2= \frac{-1\pm\sqrt {729}}2= \frac{-1\pm27}2 ,

x_1=-14, x_2=13.

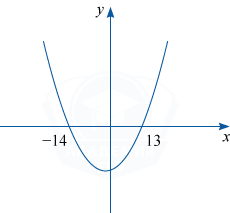
Ветви параболы y=x^2+x-182 направлены вверх, эскиз графика имеет вид, изображённый на рисунке.

Неравенство выполнено, если -14 \leqslant x \leqslant 13.

С учётом ограничения x>5 получим, что наибольшим целым значением x, удовлетворяющим неравенству будет x=13.

13

Ясно, что за 6 месяцев Тамара не сможет выплатить долг, т.к. вернёт банку не более 250\,000\cdot 6=1\,500\,000 руб., а общий долг будет больше 1,5 млн, так как банк ещё начисляет проценты. Покажем, что Тамара выплатит весь долг за 7 месяцев.

Пусть все ежемесячные платежи, кроме, быть может, последнего, равны 250 тысяч рублей. Через месяц долг Тамары перед банком составит 1\,500\,000\cdot 1,01=1\,515\,000 руб. Затем Тамара выплатит 250\,000 и задолженность составит 1\,265\,000 руб. После этого банк начислит проценты, но 1% от оставшейся суммы будет уже меньше 15\,000 руб., а в дальнейшем будет становиться ещё меньше, так как сумма долга будет уменьшаться. Поэтому долг через 2 месяца будет менее 1\,280\,000 а после очередного платежа — менее 1\,030\,000. Аналогично через 3 месяца задолженность будет менее 1\,045\,000 руб., а после платежа — менее 795\,000 рублей. Через 4 месяца долг будет менее 810\,000 а после платежа — менее 560\,000. Через 5 месяцев долг будет менее 575\,000 а после платежа — менее 325\,000. Через 6 месяцев долг будет менее 340\,000 а после платежа — менее 90\,000 Значит, через 7 месяцев задолженность будет менее 105\,000 и Тамара своим последним платежом полностью расплатится с банком.

7

Сумма денег, полученная брокером ежедневно, можно рассматривать как функцию S(n) от номера n дня. Это функция задаётся формулой S(n)=n(1000-n) или S(n)=-n^2+1000n, она квадратичная, принимает наибольшее значение при n=-\frac{1000}{2\cdot (-1)}=500. Значит, в 500-ый день выручка брокера была наибольшей и равна она S(500)= 500\cdot (1000-500)= 500\cdot 500= 250\,000 рублей.

500-ый день, 250\,000 рублей.

Пусть в каждый из двух банков была положена сумма S. Тогда через год в каждом из двух банков будет сумма S_1=S\cdot q, где q=1+\frac r{100}. Таким образом, начисление r% годовых соответствует умножению на коэффициент q. Тогда начисление 10% годовых соответствует умножению на коэффициент 1,1. Через 3 года на вкладе в банке «A» будет сумма S_3{(A)}=S\cdot q\cdot 1,1^2, а на вкладе в банке «B» — сумма S_3(B)=S\cdot q^{3}. По условию задачи должно выполняться, неравенство S_3(B) \geqslant S_3{(A)}\cdot 1,2,

S\cdot q^3 \geqslant S\cdot q\cdot 1,1^{2}\cdot 1,2,

q^2 \geqslant 1,21\cdot 1,2. Так как 100q — целое, то q>1,2,

q\geqslant 1,21,

1+\frac r{100} \geqslant 1,21,

r\geqslant 21.

Наименьшим целым r, удовлетворяющим неравенству, будет r=21.

21

Пусть x — количество акций предприятия A, y — количество акций предприятия B.

Согласно условию задачи составим систему ограничений на переменные x и y:

\begin{cases} x+y=6000,\\ 5x+3y \leqslant 25\,000,\\ x \geqslant 1,\\ y \geqslant 1. \end{cases}

Прибыль от инвестиций составит f=1,1x+0,9y (долларов). Из уравнения системы выразим y=6000-x и подставим в выражение f=1,1x+0,9y и неравенство 5x+3y \leqslant 25\,000. Получим линейную возрастающую функцию натурального аргумента f(x)=0,2x+5400 при условии 1 \leqslant x \leqslant 3500. Наибольшее значение функции достигается при x=3500: f_{max}=0,2\cdot 3500+5400=6100. Тогда y=6000-3500=2500.

Чтобы клиенту получить максимальную прибыль, необходимо приобрести 3\,500 акций предприятия A и 2\,500 акций предприятия B.

План решения.

Заметим, что в качестве единицы измерения удобнее (но не обязательно!) взять тысячу рублей, а не рубль, чтобы не иметь дела с большими числами.

1. Найдём, при какой величине текущей суммы выгоднее выбирать первый способ начисления прибыли, а при какой — второй. Определим, что, пока текущая сумма меньше 1000 тысяч рублей, выгоднее выбирать второй способ начисления прибыли, а когда она превысит 1000 тысяч, то первый. Если сумма равна 1000 тысяч, то схемы принесут одинаковую прибыль.

2. Попробуем решить задачу, предполагая, что сумма на счёте изначально не меньше 1000 тысяч. Получим противоречие.

3. Попробуем решить задачу, предполагая, что сумма на счёте изначально меньше 1000 тысяч, но после получения прибыли за первый год станет не меньше 1000 тысяч. Если получим противоречие, предположим, что сумма на счёте станет не меньше 1000 тысяч только после получения прибыли за второй год, и так далее, пока не получим подходящее решение.

Решение.

1. Пусть текущая сумма равна S тысяч рублей, S>0.

\left( 1+\frac{10}{100} \right) S\geqslant \left( 1+\frac5{100} \right) S+50,

x\geqslant 1000.

2. Пусть Иван положил в банк x тысяч рублей, x>0.

Если x \geqslant 1000, то максимальная прибыль равна 1,1^4\cdot x-x= 1,4641x-x= 0,4641x \geqslant 464,1, что противоречит условию (по условию максимальная прибыль равна 417,967 тысяч рублей).

3.1. Если x<1000, но 1,05x+50 \geqslant 1000, то максимальная прибыль равна (1,05x+50)\cdot 1,1^3-x= 0,39755x+66,55= 417,967, x=\frac{351,417}{0,39755}<900. Но тогда 1,05x+50<1,05\cdot 900+50<1000, что противоречит предположению.

3.2. 1,05x+50<1000 и (1,05x+50)\cdot 1,05+50 \geqslant 1000. В этом случае максимальная прибыль равна

((1,05x+50)\cdot 1,05+50)\cdot 1,1^2-x= 0,334025x+124,025.

Из уравнения 0,334025x+124,025=417,967 получим: x=880 (тысяч рублей).

Убедимся, что при этом значении x выполняются неравенства 1,05x+50<1000 и (1,05x+50)\cdot 1,05+50 \geqslant 1000.

880\,000

Пусть искомый ежегодный платёж составляет x рублей, тогда в конце первого года

Иван Иванович будет должен 1,2\cdot 910\,000-x=1\,092\,000-x (рублей). Аналогично в конце второго года его долг составит 1,2(1\,092\,000-x)-x= 1\,310\,400-2,2x (рублей). В конце третьего года его долг составит 1,2(1\,310\,400-2,2x)-x= 1\,572\,480-3,64x.

По условию Иван Иванович выплатил долг тремя платежами, поэтому к концу третьего года долг составит 0 рублей, то есть 1\,572\,480-3,64x=0, x=\frac{1\,572\,480}{3,64}=432\,000 (рублей).

Итак, сумма ежегодного платежа равна 432\,000 рублей.

432\,000 рублей.

Обозначим через K сумму выданного кредита, а через x_1, x_2, x_3, x_4, x_5 и x_6 — выплаты по кредиту в апреле, мае, июне, июле, августе и сентябре. Тогда по условию на конец марта текущий долг будет равен 1,05\cdot K. После уплаты суммы x_1 он станет равным 1,05\cdot K-x_1 и будет равен 80% от K, то есть 0,8\cdot K. Составляем первое уравнение: 1,05\cdot K-x_1=0,8\cdot K.

Далее этот текущий долг опять увеличивается на 5%, и опять уплачивается сумма x_2, после чего останется 65% от K. Получаем второе уравнение:

1,05\cdot 0,8\cdot K-x_2=0,65\cdot K.

Последующие уравнения будут иметь вид:

1,05\cdot 0,65\cdot K-x_3=0,45\cdot K;

1,05\cdot 0,45\cdot K-x_4=0,3\cdot K;

1,05\cdot 0,3\cdot K-x_5=0,2\cdot K;

1,05\cdot 0,2\cdot K-x_6=0.

Складывая полученные уравнения, имеем:

1,05K\,\cdot (1+0,8+0,65+0,45+0,3+0,2)\,\,- (x_1+x_2+x_3+x_4+x_5+x_6)= K\cdot (0,8+0,65+0,45+0,3+0,2).

Отсюда x_1 +x_2 +x_3 +x_4 +x_5 +x_6= K\cdot (1,05+0,05\cdot (0,8+0,65+0,45+0,3+0,2))= K\cdot (1,05+0,05\cdot 2,4)= K\cdot (1,05+0,12)= K\cdot 1,17.

Получаем, что сумма всех выплат больше суммы кредита на 0,17K, то есть на 17% от K.

17

Пусть x млн рублей инвестировано в производство, тогда в банке размещено (400-x) млн рублей.

Деньги в банке размещены под 12% годовых, поэтому через год в банке станет 1,12(400-x) млн рублей.

По условию через год эффективность вложения в производство ожидается в размере 250%, то есть вложенные x млн рублей превратятся в 2,5x млн рублей. Теперь от 2,5x нужно вычесть деньги на издержки, которые задаются квадратичной зависимостью: (2,5x-0,0022x^2 ) млн рублей, после чего нужно заплатить налог в 20% от этой суммы, поэтому останется 80% этой суммы, то есть 0,8\cdot (2,5x-0,0022x^2 ) млн рублей.

Рассмотрим функцию прибыли

f(x)= 1,12(400-x)\,\,+ 0,8\cdot (2,5x-0,0022x^2 )-400,

f(x)= 448-1,12x+2x-0,8\cdot 0,0022x^2-400,

f(x)=-0,8\cdot 0,0022x^2+0,88x+48.

Это квадратичная функция, наибольшее значение она принимает в точке x= \frac{-0,88}{2\cdot (-0,8\cdot 0,0022)} = \frac{88000}{2\cdot 8\cdot 22}= 250.

f(250)= -0,8\cdot 0,0022\cdot 250^2+0,88\cdot 250+48= -110+220+48= 158 (млн рублей).

Итак, прибыль составит 158 млн рублей.

158

Составим математическую модель задачи. Увеличение вклада на 10% означает умножение начальной суммы на 1,1.

Пусть первоначальный вклад равен P десятков тысяч рублей. Тогда в конце первого года вклад составил 1,1P+3, а в начале второго года (1,1P+3)\cdot 1,1 десятков тысяч рублей. В начале третьего года —  (1,1P+3)\cdot 1,1+3, а в конце третьего года —

((1,1P+3)\cdot 1,1+3)\cdot 1,1 десятков тысяч рублей.

По условию нужно найти наибольшее целое число P такое, чтобы через три года вклад был меньше 9,6 десятков тысяч рублей, то есть было выполнено неравенство

((1,1P+3)\cdot 1,1+3)\cdot 1,1<9,6.

Решим это неравенство и найдём наибольшее целое решение этого неравенства.

(1,1^2 P+3\cdot 1,1+3)\cdot 1,1<9,6,

1,1^3 P+3\cdot 1,1^2 +3\cdot 1,1<9,6,

1,1^3 P<2,67.

P<\frac{2,67}{1,331} , P<\frac{2670}{1331} , P<\frac8{1331}.

Наибольшее целое решение этого неравенства — число 2. Значит, размер первоначального вклада составляет 20 000 рублей.

20\,000