Задания по теме «Задачи с параметром»

Если y \geqslant 0, то первое уравнение задаёт окружность \phi _1 с центром в точке C_1(4; 4) радиуса 3, а если y < 0, то оно задаёт окружность \phi _2 с центром в точке C_2(4; -4) того же радиуса.

При a > 0 второе уравнение задаёт окружность \phi с центром в точке C(0; 4) радиуса a. Поэтому задача состоит в том, чтобы найти все значения параметра a, при каждом из которых окружность \phi имеет ровно две общие точки с объединением окружностей \phi _1 и \phi _2.

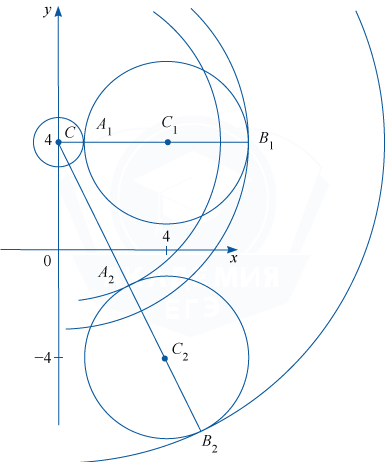
Координаты точки касания окружностей \phi и \phi _1 явно видны на чертеже — точки A_1(1; 4) и B_1(7; 4). То есть при a=CA_1=1 и a=CB_1=7 окружности \phi и \phi _1 касаются. При a > 7 и a < 1 окружности \phi и \phi _1 не пересекаются, при 1 < a < 7 окружности \phi и \phi _2 имеют 2 общие точки.

Далее, из точки C проведём луч CC_2 и обозначим A_2 и B_2 точки его пересечения с окружностью \phi_2 , где A_2 лежит между C и C_2. Заметим, что длина отрезка CC_2= \sqrt {4^2+(4-(-4))^{2}}= \sqrt {80}= 4\sqrt 5.

При a < CA_2 или a > CB_2 окружности \phi и \phi_2 не пересекаются. При CA_2 < a < CB_2 окружности \phi и \phi _2 имеют 2 общие точки. При a =CA_2=4\sqrt 5-3 или a=CB_2=4\sqrt 5+3, окружности \phi и \phi _2 касаются.

Исходная система имеет ровно 2 решения тогда и только тогда, когда окружность \phi с одной из окружностей \phi _1 и \phi _2 имеет 2 общие точки, а с другой не пересекается, либо касается одновременно двух окружностей.

Так как 1<4\sqrt 5-3<7<4\sqrt 5+3, то условию задачи удовлетворяют значения a\in(1;4\sqrt 5-3) \cup (7; 4\sqrt 5+3).

(1;4\sqrt 5-3) \cup  (7; 4\sqrt 5+3).

Преобразуем второе уравнение системы, выделив полные квадраты:

\begin{cases}15|x-2|+8|y+3|=120,\\ x^2-4a^2+2y+5=4(x-1)-(y+2)^2 ;\end{cases}

\begin{cases}15|x-2|+8|y+3|=120,\\ (x^2- 4x+4)+(y^2+6y+9)=(2a)^2 ;\end{cases}

\begin{cases}15|x-2|+8|y+3|=120,\\ (x-2)^2 +(y+3)^2 =(2a)^2.\end{cases}

Сделав замену переменных t=x-2 и \omega=y+3, получим систему:

\begin{cases}15|t|+8|\omega |=120,\enspace (1) \\ t^2 +\omega^2 =(2a)^2.\enspace(2) \end{cases}

При такой замене старая и новая система имеют одинаковое число решений.

Построим графики уравнений (1) и (2) в системе координат Ot\omega.

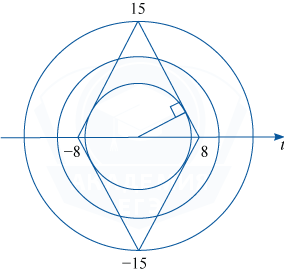
График уравнения (1) — ромб, диагонали которого, равные 16 и 30, лежат соответственно на осях Ot и O\omega , а графиком уравнения (2) является семейство окружностей с центром в начале координат и радиусом r=2|a|.

Графики уравнений системы имеют ровно 4 общие точки, и следовательно система имеет ровно 4 решения тогда и только тогда, когда окружность либо вписана в ромб, либо её радиус удовлетворяет условию: 8<r<15.

В первом случае радиус окружности является высотой прямоугольного треугольника с катетами 8 и 15, откуда

r=2|a|=\frac{8\cdot 15}{\sqrt {8^2 +15^2 }}=\frac{120}{17} ,

|a|=\frac{60}{17}=3\frac9{17} , тогда a=\pm3\frac9{17}.

Во втором случае получаем 8<2|a|<15, откуда -7,5<a<-4 или 4<a<7,5.

a \in (-7,5; -4) \cup  \left\{\pm3\frac9{17} \right\} \cup  (4; 7,5).

Если x \geqslant 0, то первое уравнение задаёт окружность \phi _1 с центром в точке C_1(3; 3) радиуса 2, а если x<0, то оно задаёт окружность \phi _2 с центром в точке C_2(-3; 3) того же радиуса.

При a>0 второе уравнение задаёт окружность \phi с центром в точке C(-3; 0) радиуса a. Поэтому задача состоит в том, чтобы найти все значения параметра a, при каждом из которых окружность \phi имеет единственную общую точку с объединением окружностей \phi _1 и \phi _2.

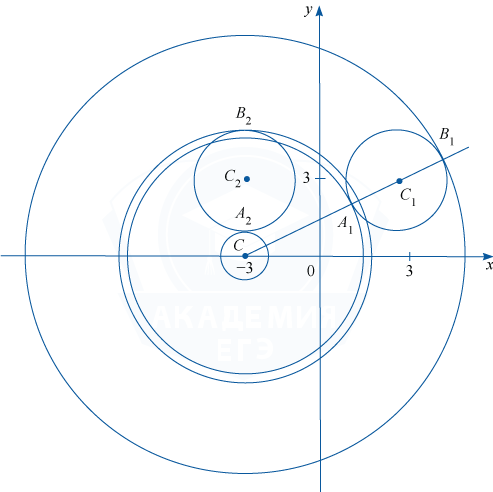
Из точки C проведём луч CC_1 и обозначим A_1 и B_1 точки его пересечения с окружностью \phi _1, где A_1 лежит между C и C_1.

Так как CC_1=\sqrt {6^2 +3^2 }=\sqrt {45} =3\sqrt 5, то CA_1=3\sqrt 5-2, CB_1=3\sqrt 5+2.

При a < CA_1 или a > CB_1 окружности \phi и \phi _1 касаются. При CA_1 < a < CB_1 окружности \phi и \phi _1 имеют 2 общие точки. При a=CA_1=3\sqrt 5-2 или a=CB_1=3\sqrt 5+2, окружности \phi и \phi _1 касаются.

Координаты точки касания окружностей \phi и \phi _2 явно видны на чертеже: это точки A_2(-3; 1) и B_2(-3; 5). То есть при a=1 и a=5 окружности \phi и \phi _2 касаются. При остальных значениях параметра a окружности \phi и \phi _2 либо имеют 2 общие точки, либо не имеют общих точек.

Исходная система имеет единственное решение тогда и только тогда, когда окружность \phi касается ровно одной из двух окружностей \phi _1 и \phi _2 и не пересекается с другой.

Так как 1<3\sqrt 5-2<5<3\sqrt 5+2, то условию задачи удовлетворяют только числа a=1 и a=3\sqrt 5+2.

1; 3\sqrt 5+2.

Рассмотрим первое уравнение системы. Выражение AB=\sqrt {(x-3)^2 +y^2 } определяет расстояние между точками A(x; y) и B(3; 0). Аналогично выражение AC=\sqrt {x^2+(y-a)^2 } определяет расстояние между точками A(x; y) и C(0; a), а выражение BC=\sqrt {a^2 +9} определяет расстояние между точками B(3;0) и C(0; a).

По неравенству треугольника AB+AC \geqslant BC, причём равенство достигается тогда и только тогда, когда точка A принадлежит отрезку BC. Это значит, что для координат точки A(x; y) справедливы неравенства: 0 \leqslant x \leqslant 3, 0 \leqslant y \leqslant a.

Тогда из второго уравнения системы имеем:

0\leqslant |2-a^2 |\leqslant a, |2-a^2 |\leqslant a, -a\leqslant 2-a^2 \leqslant a,\begin{cases} 2-a^2 \geqslant -a,\\2-a^2 \leqslant a, \end{cases} \enspace \begin{cases} a^2 -a-2\leqslant 0,\\a^2+a-2\geqslant 0, \end{cases} \enspace \begin{cases} -1\leqslant a\leqslant 2,\\a\leqslant -2, a\geqslant 1, \end{cases}\enspace a\in[1;2].

Итак, первое уравнение системы определяет на плоскости xOy отрезок с концами в точках B и C, не параллельный оси Ox; второе уравнение системы определяет прямую, параллельную оси Ox. При a \in [1; 2] они имеют одну точку пересечения, то есть исходная система уравнений имеет единственное решение.

[1; 2].

Решим задачу графически. Если |5-2a|=0, то неравенство системы задаёт круг с центром в точке (2a; \cos \pi a) и радиусом |5a-21|. Если |5a-21|=0, то решением

неравенства будет единственная точка: x=2a=\frac{42}5 , y=\cos \pi a=\cos \frac{21\pi }5 , а тогда у системы не может быть более одного решения.

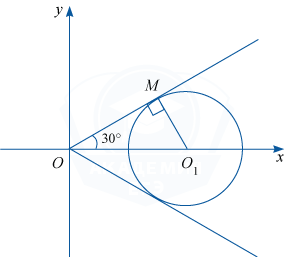
Уравнение системы задаёт угол, биссектрисой которого является ось Ox. Сторона этого угла проходит через точки (0; 0) и \left(1; \frac1{\sqrt 3}\right), и поэтому образует угол 30^{\circ} с положительным направлением оси Ox.

Ровно два решения будет, если круг касается обеих сторон угла. Тогда центр круга должен лежать на биссектрисе угла, то есть на луче Ox. Следовательно, ордината центра круга должна равняться нулю, а абсцисса быть больше нуля. Ордината равна нулю, если \cos \pi a=0, \pi a=\frac \pi 2+\pi k, k \in \mathbb Z, a=\frac12+k, k ∈ Z.

Абсцисса центра круга равна 2a и равна 2k+1, она больше нуля, если k \geqslant 0. Рассмотрим \triangle O_1OM , где O_1 — центр круга, M — одна из точек касания. Тогда O_1M=|5a-21|, OO_1=2a, \angle O_1MO =90^{\circ}, \angle MOO_1 =30^{\circ}. Тогда O_1M= O_1O\cdot \sin \angle O_1OM= 2a\sin 30^{\circ}= a. Значит, a=|5a-21|, k+\frac12= \left|5k+\frac52 -21\right|, k+\frac12=\left|5k-\frac{37}2 \right|; отсюда либо k+\frac12 =5k-\frac{37}{2,} то есть 4k=19,\, k=\frac{19}4 ; либо k+\frac12 =\frac{37}2-5k,\, 6k=18, k=3. k — целое число, \frac{19}4 \notin Z. 3\in \mathbb Z и 3\geqslant 0. Таким образом, k=3, a=\frac12+k=3,5.

3,5

Уравнение \frac{x^2+ax+2}2=\sqrt {4x^2+ax+1} при \frac{x^2+ax+2}2<0 не имеет корней. При x^2+ax+2 \geqslant 0 обе части уравнения можно возвести в квадрат.

(x^2+ax+2)^2 =4(4x^2+ax+1),

x^4+ax^3+2x^2+ax^3+a^2x^2\,+ 2ax+2x^2+2ax+4= 16x^2+4ax+4,

x^4+2ax^3+x^2(a^2-12)=0,

x^2(x^2+2ax+a^2-12)=0,

x^2((x+a)^2-12) =0,

x_1=0, (x+a-\sqrt {12})(x+a+\sqrt {12})=0,

x_2=-a+\sqrt {12},

x_3=-a-\sqrt {12}.

Чтобы исходное уравнение имело три различных корня, необходимо, чтобы числа x_{1,} x_{2,} x_3 были различными и для каждого из этих чисел выполнялось условие x^2 +ax+2 \geqslant 0.

x_2 \neq 0 и x_3 \neq 0, если a \neq \sqrt {12}=2\sqrt 3 и a \neq -\sqrt {12}=-2\sqrt 3.

Обозначим g(x)=x^2+ax+2. g(0)=2>0. Числа x_2=-a+2\sqrt 3 и x_3=-a-2\sqrt 3 будут корнями исходного уравнения, если выполняются условия:

\begin{cases} g(x_2)\geqslant 0,\\g(x_3)\geqslant 0; \end{cases}\enspace \begin{cases} (-a+2\sqrt 3)^2+a(-a+2\sqrt 3)+2\geqslant 0,\\( -a-2\sqrt 3)^2+a(-a-2\sqrt 3)+2\geqslant 0; \end{cases}

\begin{cases} -2a\sqrt 3+14\geqslant 0,\\2a\sqrt 3+14\geqslant 0; \end{cases}\enspace \begin{cases} a\leqslant \frac7{\sqrt 3} ,\\a\geqslant -\frac7{\sqrt 3}. \end{cases}

Таким образом, a\in\left[-\frac7{\sqrt3};-2\sqrt3\right)\,\cup (-2\sqrt 3;2\sqrt3)\,\,\,\cup \left( 2\sqrt3;\frac7{\sqrt3}\right].

\left[-\frac7{\sqrt3};-2\sqrt3\right)\,\cup (-2\sqrt3;2\sqrt3)\,\,\,\cup \left(2\sqrt3;\frac7{\sqrt3}\right].

Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.

Первое уравнение \frac{xy^2-5xy-5y+25}{\sqrt {x+5}}=0 параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.

Запишем уравнение в виде \frac{(y-5)(xy-5)}{\sqrt {x+5}}=0, разложив числитель на множители. При x \leqslant -5 левая часть не имеет смысла. При x>-5 уравнение задаёт прямую y=5 и гиперболу y=\frac5x.

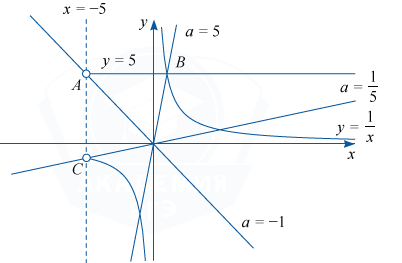
Найдём координаты точек A, B и C. B — точка пересечения прямой y=5 и гиперболы y=\frac5x , чтобы найти её координаты, нужно решить систему уравнений \begin{cases} y=5,\\y=\frac5x. \end{cases}

Получаем B(1; 5).

У точек A и C абсцисса равна -5, ординаты находим из уравнений прямой и гиперболы. A(-5;5) и C(-5;-1).

При каждом значении a уравнение y=ax задаёт прямую с угловым коэффициентом a, проходящую через начало координат. Чтобы найти значение a, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.

Например, для точки A(-5; 5) получаем x=-5, y=5, 5=a\cdot (-5), a=-1.

Аналогично для B(1;5),\, a=5 и для C(-5;-1), a=\frac15.

При x>-5 прямая y=ax пересекает прямую y=5 при a<-1 и a>0, пересекает правую ветвь гиперболы y=\frac5x при a>0, пересекает левую ветвь гиперболы y=\frac5x при a>\frac15. При этом прямая y=ax проходит через точку пересечения прямой y=5 и гиперболы y=\frac5x при a=5.

Число решений исходной системы равно числу точек пересечения прямой y=5 и гиперболы y=\frac5x с прямой y=ax при условии x>-5.

Таким образом, исходная система имеет ровно два решения при 0 < a \leqslant 0,2; a=5.

(0; 0,2]; \{5\}.

\frac{(x-3a)(x-a)+(x+3)(x-2)-(x+3)(x-a)}{(x+3)(x-a)}=0,

\frac{x^2-ax-3ax+3a^2+x^2+x-6-x^2+ax-3x+3a}{(x+3)(x-a)}=0,

\frac{x^2-x(3a+2)+3a^2+3a-6}{(x+3)(x-a)}=0,

\begin{cases} x^2-x(3a+2)+3a^2+3a-6=0,\\(x+3)(x-a)\neq 0 \end{cases}

Решим уравнение x^2-x(3a+2)+3a^2+3a-6=0,

x_{1,2}=\frac{(3a+2)\pm\sqrt {-3a^2+28}}2.

1. При D<0 уравнение корней не имеет.

2. При D=0,\enspace -3a^2+28=0, a=\pm 2\sqrt \frac73. Уравнение имеет единственный корень x =\frac{3a+2}2 при a=\pm 2 \sqrt \frac73.

Проверим условие x \neq -3,\, x \neq a.

\frac{3a+2}2 =-3, a=-\frac83 \neq \pm2\sqrt \frac73 ,

\frac{3a+2}2 =a, a=-2\neq \pm2\sqrt \frac73.

Значит, a=\pm 2\sqrt \frac73 удовлетворяет условию.

3. При D>0 уравнение имеет два корня x_{1,2}=\frac{(3a+2) \pm \sqrt {28-3a^2}}2. Проверим, при каких значениях a значения x=-3 и x=a являются корнями уравнения x^2-x(3a+2)+3a^2+3a-6=0.

При x=-3 должно выполняться равенство 9+3(3a+2)+3a^2+3a-6=0,

3a^2+12a+9=0, a^2+4a+3=0, a=-1, a=-3.

При x=a должно выполняться равенство a^2-2a+3a-6=0,

a^2+a-6=0, a_1=-3, a_2=2.

При a=-3, a=-1 и a=2 исходное уравнение имеет единственный корень.

 -3;  −1; \pm 2\sqrt \frac73 ;  2.

Преобразуем второе уравнение системы, выделив полный квадрат y^2-4y+4=(y-2)^2.

\begin{cases} 5|x|+12|y-2|=60, \\ y^2-a^2=4(y-1)-x^2;\end{cases} \Leftrightarrow \begin{cases}5|x|+12|y-2|=60, \\ x^2+(y-2)^2=a^2. \end{cases}

Сделав замену переменных t=y-2, получим систему

\begin{cases} 5|x|+12|t|=60,\enspace(1)\\ x^2+t^2=a^2.\enspace(2)\end{cases}

При такой замене число решений новой и старой системы одинаково. Построим графики уравнений (1) и (2) в системе координат Oxt.

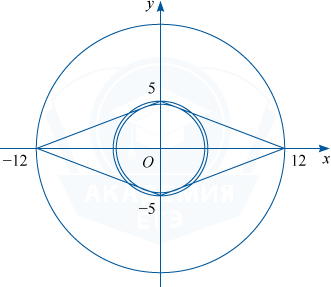
График уравнения (1) — ромб, диагнали которого, равные 24 и 10, лежат соответственно на осях Ox и Ot, а графиком уравнения (2) является семейство окружностей с центром в начале координат и радиусом r=|a|.

Графики уравнений системы имеют ровно 4 общие точки, и следовательно, система имеет ровно 4 решения тогда и только тогда, когда окружность либо вписана в ромб, либо её радиус удовлетворяет условию 5 < r < 12.

В первом случае радиус окружности является высотой прямоугольного треугольника с катетами 5 и 12, откуда

r=|a|=\frac{5 \cdot 12}{\sqrt{5^2+12^2}}=\frac{60}{13}=4\frac{8}{13}, a=\pm 4\frac{8}{13}.

Во втором случае получаем 5 < |a| < 12, откуда -12 < a < -5 или 5 < a < 12.

a \in (-12;-5) \cup \left \{ \pm 4\frac{8}{13}\right \} \cup (5;12).

Уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2], если графики функций y=x^3+3x^2 и y=x\log_{3}(a+1)-5 имеют единственную точку пересечения на отрезке [0;2].

Построим графики этих функций.

1) y=x^3+3x^2.

Найдём стационарные точки: y'=3x^2+6x=3x(x+2). y'=0 при x=0, x=-2

y(-2)=-8+3(-2)^2=-8+12=4, y(0)=0. Отсюда получаем график y=x^3+3x^2.

2) y=x\log_{3}(a+1)-5. Графиком функции является прямая, угловой коэффициент которой k=\log_{3}(a+1). Прямая y=kx-5 проходит через точку (0;-5).

Найдём точку x_{0}, в которой прямая y=kx-5 является касательной к графику функции y=x^3+3x^2.

Уравнение касательной y=(x_{0}^3+3x_{0}^2)+(3x_{0}^2+6x_{0})(x-x_{0}) проходит через точку (0;-5), следовательно, -5=(x_{0}^3+3x_{0}^2)-x_{0}(3x_{0}^2+6x_{0}),

2x_{0}^3+3x_{0}^2-5=0. x_{0}=1 — точка касания.

2x_{0}^3+3x_{0}^2-5=(x_{0}-1)(2x_{0}^2+5x_{0}+5).

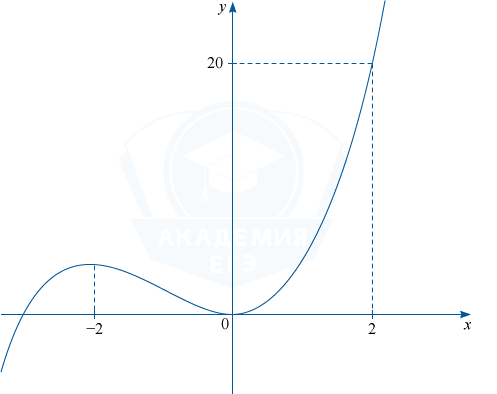
Других точек касания нет, так как уравнение 2x_{0}^2+5x_{0}+5=0 корней не имеет.

Если x=1, то y=4, тогда 4=k-5, откуда k=9.

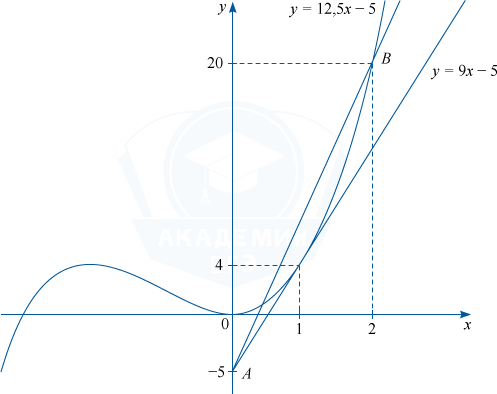
Найдем значение k, при котором прямая y=kx-5 проходит через точку (2;20). 20=2k-5, k=12,5, y=12,5x-5.

Для k=9 и k > 12,5 графики функций y=x^3+3x^2 и y=kx-5 имеют на отрезке [0;2] единственную общую точку. Найдем значения параметра a.

\log_{3}(a+1)=9, a+1=3^9, a=3^9-1.

\log_{3}(a+1) > 12,5, a+1 > 3^{\tfrac{25}{2}}. a > 3^{12,5}-1.

Итак, если a=3^9-1 или a > 3^{12,5}-1, то уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2].

a=3^9-1,\, a > 3^{12,5}-1