Задание №1018

Уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2], если графики функций y=x^3+3x^2 и y=x\log_{3}(a+1)-5 имеют единственную точку пересечения на отрезке [0;2].

Построим графики этих функций.

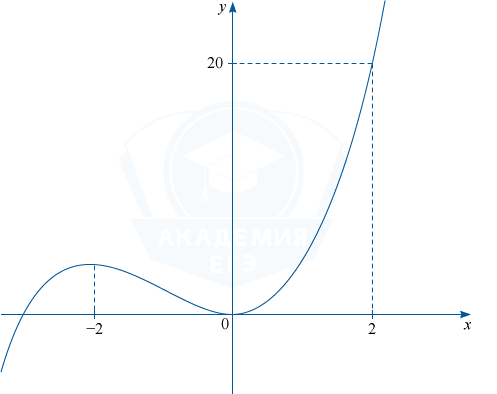
1) y=x^3+3x^2.

Найдём стационарные точки: y'=3x^2+6x=3x(x+2). y'=0 при x=0, x=-2

y(-2)=-8+3(-2)^2=-8+12=4, y(0)=0. Отсюда получаем график y=x^3+3x^2.

2) y=x\log_{3}(a+1)-5. Графиком функции является прямая, угловой коэффициент которой k=\log_{3}(a+1). Прямая y=kx-5 проходит через точку (0;-5).

Найдём точку x_{0}, в которой прямая y=kx-5 является касательной к графику функции y=x^3+3x^2.

Уравнение касательной y=(x_{0}^3+3x_{0}^2)+(3x_{0}^2+6x_{0})(x-x_{0}) проходит через точку (0;-5), следовательно, -5=(x_{0}^3+3x_{0}^2)-x_{0}(3x_{0}^2+6x_{0}),

2x_{0}^3+3x_{0}^2-5=0. x_{0}=1 — точка касания.

2x_{0}^3+3x_{0}^2-5=(x_{0}-1)(2x_{0}^2+5x_{0}+5).

Других точек касания нет, так как уравнение 2x_{0}^2+5x_{0}+5=0 корней не имеет.

Если x=1, то y=4, тогда 4=k-5, откуда k=9.

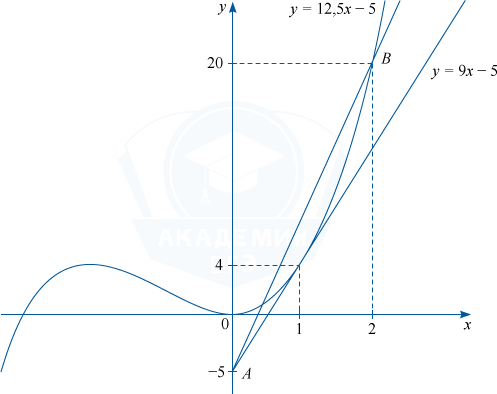
Найдем значение k, при котором прямая y=kx-5 проходит через точку (2;20). 20=2k-5, k=12,5, y=12,5x-5.

Для k=9 и k > 12,5 графики функций y=x^3+3x^2 и y=kx-5 имеют на отрезке [0;2] единственную общую точку. Найдем значения параметра a.

\log_{3}(a+1)=9, a+1=3^9, a=3^9-1.

\log_{3}(a+1) > 12,5, a+1 > 3^{\tfrac{25}{2}}. a > 3^{12,5}-1.

Итак, если a=3^9-1 или a > 3^{12,5}-1, то уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2].

a=3^9-1,\, a > 3^{12,5}-1