Задание №1017

Исходное уравнение равносильно уравнению a + \sqrt{a+\sqrt{x}}=x.

Рассмотрим функцию f(x)=a+\sqrt{x,} определённую при x \geq 0. Тогда полученное уравнение можно записать в виде f(f(x))=x. Это уравнение равносильно уравнению f(x)=f^{-1}(x), где f^{-1}(x) — функция, обратная к f(x). Если y=a+\sqrt{x}, то x=(y-a)^2. Тогда обратной к функции f(x) является функция f^{-1}(x)=(x-a)^2, определенная при x \geq a. Проверим это:

f(f^{-1}(x))= a+\sqrt{f^{-1}(x)}= a+\sqrt{(x-a)^2}= a+|x-a|= a+x-a=x

f^{-1}(f(x))= (f(x)-a)^2= (a+\sqrt{x}-a)^2=x

Возможны три случая.

1. При a > 0 уравнение f(x)=f^{-1}(x) имеет единственный корень x_{0}

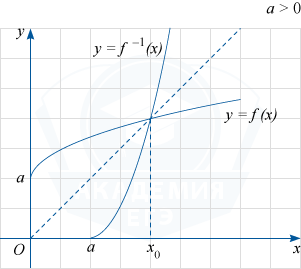
2. При a=0 уравнение f(x)=f^{-1}(x) принимает вид \sqrt{x}=x^{2} и имеет два корня: x_{1}=0 и x_{2}=1.

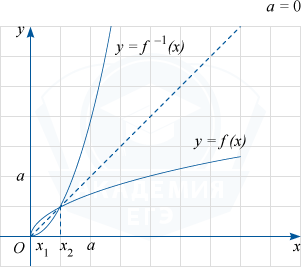
3. При a < 0 уравнение f(x)=f^{-1}(x) будет иметь один единственный корень x_{0}, только если прямая y=x будет общей касательной к графикам функций y=f(x) и y=f^{-1}(x) в точке с абсциссой x_{0}

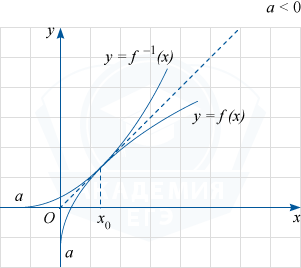
В этом случае в точке x_{0} выполняются условия:

\begin{cases} f(x_{0})=f^{-1}(x_{0}), \\ f'(x_{0})=1;\end{cases}

\begin{cases} a+\sqrt{x_{0}}=(x_{0}-a)^2, \\ \frac{1}{2\sqrt{x_{0}}}=1.\end{cases}

Из второго уравнения системы находим x_{0}=\frac{1}{4} и подставляем это значение в первое уравнение:

a=\sqrt{\frac{1}{4}}=\left ( \frac{1}{4}-a\right )^2;

a+\frac{1}{2}=\frac{1}{16}-\frac{a}{2}+a^2;

a^2-\frac{3}{2}a-\frac{7}{16}=0;

16a^2-24a-7=0.

Последнее уравнение имеет два корня: a_{1}=-\frac{1}{4} и a_{2}=\frac{7}{4}. Так как a < 0, то a=-\frac{1}{4}.

\left \{-\frac{1}{4}\right \} \cup (0;+\infty )