Задание №1226

Преобразуем второе уравнение системы, выделив полные квадраты:

\begin{cases}15|x-2|+8|y+3|=120,\\ x^2-4a^2+2y+5=4(x-1)-(y+2)^2 ;\end{cases}

\begin{cases}15|x-2|+8|y+3|=120,\\ (x^2- 4x+4)+(y^2+6y+9)=(2a)^2 ;\end{cases}

\begin{cases}15|x-2|+8|y+3|=120,\\ (x-2)^2 +(y+3)^2 =(2a)^2.\end{cases}

Сделав замену переменных t=x-2 и \omega=y+3, получим систему:

\begin{cases}15|t|+8|\omega |=120,\enspace (1) \\ t^2 +\omega^2 =(2a)^2.\enspace(2) \end{cases}

При такой замене старая и новая система имеют одинаковое число решений.

Построим графики уравнений (1) и (2) в системе координат Ot\omega.

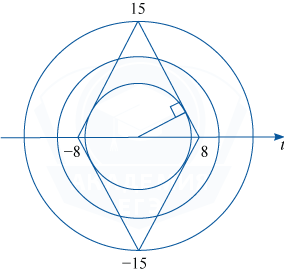
График уравнения (1) — ромб, диагонали которого, равные 16 и 30, лежат соответственно на осях Ot и O\omega , а графиком уравнения (2) является семейство окружностей с центром в начале координат и радиусом r=2|a|.

Графики уравнений системы имеют ровно 4 общие точки, и следовательно система имеет ровно 4 решения тогда и только тогда, когда окружность либо вписана в ромб, либо её радиус удовлетворяет условию: 8<r<15.

В первом случае радиус окружности является высотой прямоугольного треугольника с катетами 8 и 15, откуда

r=2|a|=\frac{8\cdot 15}{\sqrt {8^2 +15^2 }}=\frac{120}{17} ,

|a|=\frac{60}{17}=3\frac9{17} , тогда a=\pm3\frac9{17}.

Во втором случае получаем 8<2|a|<15, откуда -7,5<a<-4 или 4<a<7,5.

a \in (-7,5; -4) \cup  \left\{\pm3\frac9{17} \right\} \cup  (4; 7,5).