Задание №1219

1. Пусть x км/ч — скорость «быстрой» лодки, тогда (x-3) км/ч — скорость «медленной» лодки. Обозначим через t время движения лодок от начала движения до поворота (в часах).

2. Найдём время, затраченное «быстрой» лодкой на весь путь. Так как эта лодка сначала шла t часов против течения, то она прошла расстояние (x-2)\cdot t км. На обратный путь уже по течению она затратила время \frac{(x-2)t}{x+2} часов.

3 Аналогично, согласно условию, медленная лодка шла против течения t часов со скоростью ((x-3)-2)=(x-5) км/ч и прошла расстояние (x-5)\cdot t км. При этом x-5>0.

На обратный путь эта лодка затратила время \frac{(x-5)\cdot t}{(x-3)+2}=\frac{(x-5)\cdot t}{x-1} часов, так как шла по течению.

4. Согласно условию время движения «быстрой» лодки не менее, чем на \frac1{15} t больше времени движения «медленной» лодки. Поэтому справедливо неравенство

\frac{(x-2)t}{x+2}-\frac{(x-5)t}{x-1} \geqslant \frac1{15} t, (t>0),

\frac{x-2}{x+2}-\frac{x-5}{x-1}-\frac1{15} \geqslant 0, (x+2>0, x-1>0)

15(x-2)(x-1)-15(x-5)(x+2)\,\,- (x+2)(x-1) \geqslant 0,

15x^2-45x+30-15x^2+45x+150\,\,- x^2-x+2 \geqslant 0,

-x^2-x+182 \geqslant 0,

x^2+x-182 \leqslant 0.

Решаем неравенство графически. Находим корни трёхчлена x^2+x-182.

x_{1,2}= \frac{-1\pm \sqrt {1+4\cdot 182}}2= \frac{-1\pm\sqrt {729}}2= \frac{-1\pm27}2 ,

x_1=-14, x_2=13.

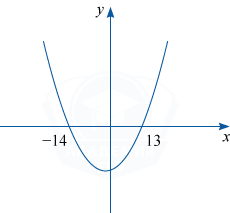
Ветви параболы y=x^2+x-182 направлены вверх, эскиз графика имеет вид, изображённый на рисунке.

Неравенство выполнено, если -14 \leqslant x \leqslant 13.

С учётом ограничения x>5 получим, что наибольшим целым значением x, удовлетворяющим неравенству будет x=13.

13