Задание №236
Условие
Равнобедренный треугольник ABC имеет стороны AB=10, AC=BC=13. В каждый угол этого треугольника вписана окружность единичного радиуса. Центрами этих окружностей являются точки O_1, O_2, O_3.
а) Найдите радиус окружности, вписанной в треугольник ABC;
б) Найдите площадь треугольника O_1O_2O_3.
Решение
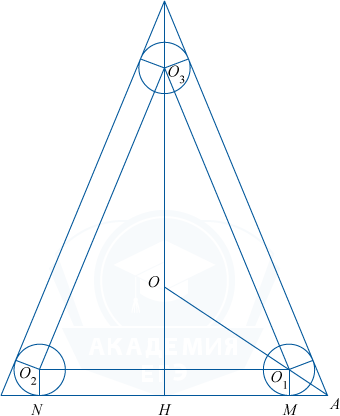
а) Высоту CH треугольника ABC можно найти по теореме Пифагора, она равна 12.
Тогда площадь S треугольника ABC равна 60, периметр P равен 36, радиус вписанной окружности равен r=\frac{2S}{P}=\frac{2 \cdot 60}{36}=\frac{10}{3}.
б) Точка O — центр окружности, вписанной в треугольник ABC, тогда OH=\frac{10}{3}. O и O_{1} лежат на биссектрисе \angle A.
Отрезки O_{1}M и O_{2}N — радиусы, проведенные в точки касания окружностей со стороной AB. OM \perp AB, \: ON \perp AB.
Треугольники AOH и AO_{1}M подобны по двум углам, поэтому их стороны пропорциональны:
\frac{OH}{O_{1}M}=\frac{AH}{AM}; \: \frac{10}{3}=\frac{5}{AM}; \: AM=1,5.
O_{1}O_{2}=MN=10-2 \cdot 1,5=7.
Треугольники ABC и O_{1}O_{2}O_{3} подобны, потому что их соответственные стороны параллельны. Коэффициент подобия k= \frac{AB}{O_{1}O_{2}}=\frac{10}{7}, поэтому площадь S_{O_{1}O_{2}O_{3}}=S_{ABC} : k^{2}=60 \cdot \frac{49}{100}=29,4
Ответ
а) \frac{10}{3};\: б) 29,4