Задание №961
Условие
В треугольнике ABC с прямым углом C MN — средняя линия, параллельная стороне AC. Биссектриса угла A пересекает луч MN в точке K.
а) Докажите, что \bigtriangleup BKC \sim \bigtriangleup AMK.
б) Найдите отношение S_{BKC}:S_{AMK}, если \cos \angle BAC=0,6.
Решение
а) В треугольнике ABC AK — биссектриса, поэтому \angle KAC=\angle AKM как накрест лежащие при MN \parallel AC и секущей AK, \angle KAM= \angle KAC =\angle AKM. Поэтому треугольник AMK — равнобедренный.
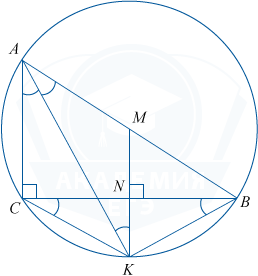
MA=MB=MK, значит, точка M — центр окружности, описанной около треугольника ABC и проходящей через точку K. MN — средняя линия треугольника ABC. MN \parallel AC, AC \perp BC. Отсюда MN \perp BC, значит, прямоугольные треугольники BNK и CNK равны по двум катетам, поэтому BK=CK и \angle KCB=\angle KBC. Равнобедренные треугольники BKC и AMK имеют равные углы при основаниях. \angle MAK=\angle BAK=\angle BCK, как вписанные, опирающиеся на одну и ту же дугу. Следовательно, они подобны по первому признаку подобия.
б) По теореме об отношении площадей подобных треугольников \frac{S_{BKC}}{S_{AMK}}=k^2, где k — коэффициент подобия, k=\frac{BC}{AK}.
Из \bigtriangleup ABC, BC= AB \cdot \sin A= 2r \cdot \sqrt{1-0,36}= 1,6r, где r — радиус окружности, описанной около треугольника ABC.
Из треугольника AMK по теореме косинусов AK^2=AM^2+MK^2- 2 \cdot AM \cdot MK \cdot \cos \angle AMK.
AK^2= r^2+r^2-2 \cdot r^2 \cdot \cos(180 ^{\circ}-\angle BMK)= 2r^2+2r^2 \cdot \cos \angle BMK.
\angle BMK= \angle BAC как соответственные при MN \parallel AC и секущей AB, значит, \cos \angle BMK=0,6.
AK=\sqrt{2r^2+2r^2 \cdot 0,6} =\sqrt{3,2r^2}, k =\frac{1,6r}{\sqrt{3,2r^2}}=\frac{1,6}{\sqrt{3,2}}.
k^2=\frac{2,56}{3,2}=\frac{256}{320}=\frac{4}{5}.
\frac{S_{BKC}}{S_{AMK}}=4:5.
Ответ
4:5