Задания по теме «Окружности и треугольники»

а) По условию \angle BAK=\angle KAD, \angle KAD=\angle AKB как накрест лежащие при BC \parallel AD и секущей AK. Следовательно, \angle BAK=\angle AKB и \triangle ABK равнобедренный.

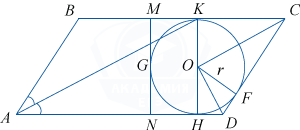
б) Пусть CF=x, FD=y, радиус окружности r, тогда, учитывая, что отрезки касательных, проведённых к окружности из одной точки, равны и треугольник ABK равнобедренный, найдём AD=2x+y, поэтому площадь параллелограмма равна S=2r(2x+y)=6(2x+y).

С другой стороны, площадь параллелограмма равна удвоенной площади прямоугольной трапеции CDNM, так как G — точка пересечения диагоналей, поэтому S= 2\cdot \frac12\cdot P_{CDNM}\cdot r= (4r+2x+2y)\cdot r= 2r(2r+x+y)= 6(6+x+y).

Приравнивая площади, получим уравнение 2x+y=6+x+y, откуда x=6.

\angle COD=90^{\circ} как угол, образованный двумя биссектрисами смежных углов. Из \triangle COD, OF^2=CF\cdot FD, r^2=x\cdot y, отсюда y=\frac{r^2}x=\frac96=\frac32.

Теперь найдём площадь параллелограмма ABCD, воспользовавшись одной из формул

S=6(2x+y)=6\left( 2\cdot 6+\frac32 \right) =81.

81

а) План решения.

1. Сделаем чертёж, считая для определённости, что AD>BC (для пункта а) это не имеет значения).

2. Заметим, что трапеция равнобедренная. Обозначим одну из сторон трапеции какой-либо буквой, выразим остальные стороны.

3. Выразим через ту же букву радиус окружности, описанной около трапеции: это можно сделать по теореме синусов для \triangle ABD.

4. Обозначим точкой N середину AD, точкой M — середину BC. Найдём CN.

5. Сравним CN с радиусом описанной окружности. Сделаем вывод, учитывая, что радиус описанной окружности лежит на прямой MN.

Решение.

1. Выполним чертёж.

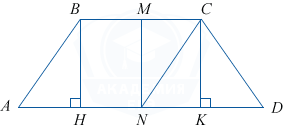
2. Так как трапеция ABCD вписана в окружность, то она равнобедренная, то есть AB=CD=a. \angle BAD=60^{\circ}. Следовательно, AH =\frac12 AB=\frac12 a, KD=\frac12 a. a. Так как в ABCD вписана окружность, то AB+CD=BC+AD, отсюда BC =\frac12 a и AD=\frac32 a.

3. Радиус описанной окружности трапеции ABCD равен радиусу описанной окружности \triangle ABD. Из \triangle ABD по теореме синусов 2R= \frac{BD}{\sin \angle BAD} = \frac2{\sqrt 3}\cdot \sqrt {BH^2+HD^2}= \frac2{\sqrt 3}\cdot \sqrt {\left( \frac{a\sqrt 3}2 \right) ^2+a^2}= \frac{\sqrt 7}{\sqrt 3} a, R=\frac{\sqrt 7}{2\sqrt 3} a.

4. Центр O описанной окружности трапеции ABCD лежит на прямой MN, где M и N — середины BC и AD соответственно. CN= \sqrt {CK^2+NK^2} = \sqrt {\left( \frac{a\sqrt 3}2 \right)^2+\left(\frac a4 \right)^2}= \frac{\sqrt {13}}4 a.

5. Сравним CN и R, \frac{\sqrt {13}}4>\frac{\sqrt 7}{2\sqrt 3,} то есть \sqrt {NM^2+MC^2}>\sqrt {OM^2+MC^2}, отсюда MN>OM или радиус описанной окружности лежит на прямой MN, а центр описанной окружности лежит внутри отрезка MN.

б) План решения.

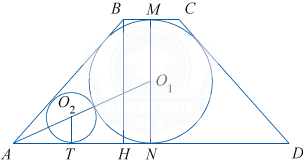
1. Сделаем чертёж, обозначив центр вписанной окружности через O_1, а центр второй окружности — через O_2. Построим радиус O_2T \perp AD.

2. Из подобных треугольников O_2AT и O_1AN, зная \angle O_2AT, вычислим O_2T.

3. Найдём искомое отношение \frac{CD}{O_2T}. 

Решение.

1. Выполним чертёж.

2. \triangle O_2AT \sim \triangle O_1AN, тогда \frac{O_1N}{O_2T}=\frac{AO_1}{AO_2}. Обозначим искомый радиус O_2T через x, получим: \frac{O_1N}x= \frac{AO_1}{AO_1-O_1N-x}. BH=MN, из \triangle ABH: BH=AB\cdot \sin 60^{\circ}=\frac{a\sqrt 3}2 , MN =\frac{a\sqrt 3}2.

Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, поэтому \angle O_1AN =\frac12 \angle BAD=30^{\circ}. Тогда AO_1=2O_1N (катет, лежащий против угла в 30^{\circ}, равен половине гипотенузы). Отсюда \frac{O_1N}x=\frac{2O_1N}{O_1N-x} , \frac1x =\frac2{O_1N-x} , O_1N-x=2x, x= \frac13 O_1N= \frac13\cdot \frac12 MN= \frac16\cdot \frac {a\sqrt 3} 2= \frac{a\sqrt 3}{12} , x=\frac{a\sqrt 3}{12} , то есть O_2T=\frac{a\sqrt 3}{12}.

3. \frac{CD}{O_2T} = \frac a{\left( \dfrac{a\sqrt 3}{12} \right)} = 4\sqrt 3.

4\sqrt 3.

1. Опишем окружность около треугольника ADC. Так как \angle ADC=120^{\circ}, то он опирается на дугу этой окружности, градусная мера которой равна 240^{\circ}.

Пусть точка M является серединой этой дуги, тогда все дуги AC, AM и CM имеют градусную меру 120^{\circ}. Поэтому треугольник AMC является равносторонним, длина каждой его стороны равна длине AC. Значит, точка M совпадает с точкой B треугольника ABC.

Получаем, что указанная окружность описана около треугольника ABC. Её центр O является точкой пересечения биссектрис (высот и медиан). Поэтому отрезок, проведённый из точки A к точке пересечения высот треугольника совпадает с отрезком AO, где AO — радиус описанной окружности. По условию l \perp OA.

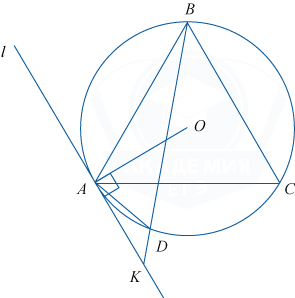
Так как l \perp AO, то l перпендикулярна радиусу, поэтому l является касательной к окружности. По свойству касательной и секущей, проведённых к окружности из одной точки K получаем: AK^2=KB\cdot KD. Но AK=1, значит 1=KB\cdot KD. Что и требовалось доказать.

б) 1. На рисунке \angle KAB=\angle KAO+\angle OAB. \angle KAO=90^{\circ} по условию, \angle OAB=\frac12\angle CAB, так как AO — биссектриса \angle CAB. Но \angle CAB=60^{\circ}, значит, \angle OAB=30^{\circ}, а \angle KAB=90^{\circ}+30^{\circ}=120^{\circ}.

2. По теореме косинусов для \triangle ABK получаем:

BK^2= AB^2+AK^2-2\cdot AB\cdot AK\cdot \cos 120^{\circ}= 4+1-2\cdot 2\cdot 1\left( -\frac12\right) = 7, так как \cos 120^{\circ}=-\frac12, BK=\sqrt 7.

В пункте а) установлено, что BK\cdot KD=1, поэтому KD=\frac1{BK}=\frac1{\sqrt 7}.

Отсюда BD=BK-KD=\sqrt 7-\frac1{\sqrt 7}=\frac6{\sqrt 7}.

Заметим, что \angle ADB =\frac12\cdot 120^{\circ}=60^{\circ} (применили теорему о вписанном угле).

3. Обозначим AD=x.

По теореме косинусов для треугольника ADB получаем: AB^2= AD^2+BD^2-2\cdot AD\cdot BD\cdot \cos \angle ADB,

4=x^2+\frac{36}7-2\cdot x\cdot\frac6{\sqrt 7}\cdot\cos 60^{\circ},

4=x^2+\frac{36}7-2\cdot x\cdot \frac6{\sqrt 7}\cdot \frac12,

x^2-\frac6{\sqrt 7}x+\frac87=0.

По теореме Виета x_1 =\frac2{\sqrt 7}, x_2=\frac4{\sqrt 7}.

По свойству треугольника DK+AK>AD, поэтому \frac1{\sqrt 7}+1>AD.

Если AD =\frac4{\sqrt 7}, то должно выполняться \frac1{\sqrt 7} +1>\frac4{\sqrt 7}, \frac3{\sqrt 7}<1, 3<\sqrt 7, что не верно.

Следовательно, AD =\frac2{\sqrt 7}.

\frac2{\sqrt7}.

а) Пусть O_1 и O_2 — центры касающихся окружностей. Через точку P проведём общую касательную заданных окружностей и обозначим через Q точку пересечения этой касательной с прямой MN.

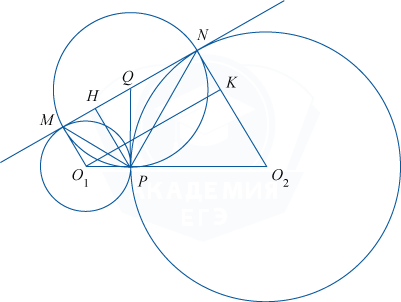
По свойству касательных, проведённых к окружности, будем иметь: QM=QP, QN=QP. Значит, точки M, N и P равноудалены от точки Q, следовательно, \angle MPN является вписанным в некоторую окружность с центром в точке Q и радиусом R=MQ. При этом \angle MPN опирается на диаметр MN, а значит, \angle MPN=90^{\circ}. Отсюда \triangle MNP является прямоугольным.

б) Пусть O_1 — центр окружности радиуса 4, а O_2 — центр окружности радиуса 16.

Рассмотрим MNO_2O_1: прямая MN — касательная к исходным окружностям, O_1M и

O_2N — радиусы, следовательно, O_1M \perp MN и O_2N \perp MN. Отсюда O_1M \parallel O_2N, а значит MNO_2O_1 — прямоугольная трапеция.

Точка касания двух окружностей лежит на линии их центров, поэтому отрезок

O_1O_2 пересекает касательную PQ в точке P, следовательно, O_1P=O_1M=4, O_2P=O_2N=16, O_1O_2=O_1P+O_2P=4+16=20.

Проведём из точки P перпендикуляр PH к отрезку MN.

Очевидно, что S_{\triangle MPH}=S_{MNO_2O_1}-S_{\triangle MPO_1}-S_{\triangle MPO_2}.

Приведем отрезок O_1K\perp NO_2, K\in NO_2, получим прямоугольник MNKO_1, в котором MN=O_1K и KN=O_1M=4, а также прямоугольный \triangle O_1KO_2, в котором KO_2=NO_2-NK=16-4=12.

Следовательно, по теореме Пифагора O_1K= \sqrt {O_1O_2^2-KO_2^2}= \sqrt {20^2-12^2}= 16,  MN-O_1K=16.

По теореме Фалеса \frac{MH}{MN}=\frac{O_1P}{O_1O_2}, следовательно, MH =\frac{MN\cdot O_1P}{O_1O_2}=\frac{16\cdot 4}{20}=\frac{16}5, отсюда NH=MN-MH=16-\frac{16}5=\frac{64}5.

S_{MNO_2O_1}= \frac{MO_1+NO_2}{2}\cdot MN= \frac{4+16}2\cdot 16= \frac{20}2\cdot 16= 160.

MH равна высоте треугольника MPO_1, опущенной на сторону MO_1.

S_{\triangle MPO_1}= \frac{MH\cdot MO_1}2 = \frac{\dfrac{16}5\cdot 4}{2}= 6,4.

NH равна высоте треугольника NPO_2, опущенной на сторону NO_2.

S_{\triangle MPO_2}= \frac{NH\cdot NO_2}2= \frac{\dfrac{64}5\cdot 16}{2}= 102,4.

Значит, S_{\triangle MPN}=160-6,4-102,4=51,2.

51,2.

а) AK — биссектриса угла \angle BAD, значит, \angle BAK=\angle KAH. Основания AD и BC трапеции параллельны, значит, \angle KAH=\angle AKB (как накрест лежащие). Поэтому \angle BAK=\angle AKB, и треугольник ABK равнобедренный.

б) Пусть CF=x, FD=y, радиус окружности r, тогда, учитывая, что отрезки касательных, проведённых к окружности из одной точки, равны и треугольник ABK равнобедренный, BC=2x+y.

С другой стороны, учитывая, что точка M — середина основания BC, получим BC=2x+2r, поэтому y=2r=4.

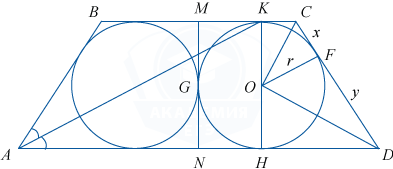
\angle COD=90^{\circ} как угол, образованный двумя биссектрисами смежных углов. Из \triangle COD, OF^2=CF\cdot FD, r^2=xy, но  y=2r. Тогда r=2x, x=1.

Найдём основания трапеции BC=2(x+r)=2\cdot (1+2)=6, AD=2(y+r)=2\cdot (4+2)=12. KH=2r=4

S= \frac12(BC+AD)\cdot KH= \frac12\cdot (6+12)\cdot 4= 36.

36

а) Доказательство.

По условию MF:MN=1:3, то есть MF=\frac13MN.

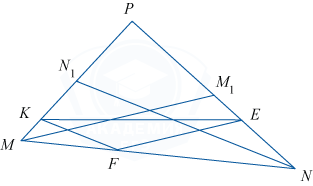
По свойству параллельных линий, отсекающих пропорциональные отрезки на пересекаемых прямых, имеем MK =\frac13MN_1, MN_1=N_1P, значит, MN_1 =\frac12MP, MK =\frac16MP;

NE =\frac23NM_1, NM_1=M_1P, NE =\frac26PN =\frac13PN.

Что и требовалось доказать.

б) S_{FEK}= S_{MNP}-(S_{MKF}+S_{KPE}+S_{FEN}).

S_{MNP}=48; S_{MKF} = \frac12MK\cdot MF \sin \angle M= \frac12MP\cdot MN \sin \angle M\cdot \frac16\cdot \frac13= S_{MNP}\cdot \frac1{18}= 48\cdot \frac1{18} = \frac{24}9=\frac83.

S_{KPE}= \frac12KP\cdot PE \sin \angle P= \frac12MP\cdot PN \sin \angle P\cdot \frac56\cdot \frac23= S_{MNP}\cdot \frac{10}{18}= S_{MNP}\cdot \frac59= 48\cdot \frac59= \frac{80}3.

S_{FEN}= \frac12FN\cdot NE \sin \angle N= \frac12MN\cdot PN \sin \angle N\cdot \frac23\cdot \frac13= S_{MNP}\cdot \frac29= \frac{32}{3}.

S_{FEK}=48-\left( \frac83+\frac{80}3+\frac{32}3\right) =8.

8

а) Рассмотрим рисунок.

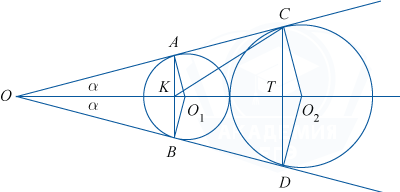
На нём O_1 и O_2 — центры окружностей (по свойству вписанной в угол окружности точки O_1 и O_2 лежат на биссектрисе \angle AOB), K и T — точки пересечения соответственно AB и CD с биссектрисой. O_1A и O_2C — радиусы окружностей, перпендикулярные касательной AC.

\triangle O_1AO=\triangle O_1BO по общей гипотенузе и острому углу, поэтому AO=BO. Таким образом, треугольник AOB является равнобедренным, и биссектриса OK угла O является высотой и медианой, поэтому точка K является серединой отрезка AB. Это и означает, что прямая AB перпендикулярна биссектрисе \angle AOB.

б) Пусть \angle AOO_1 равен \alpha. Проведём через O_1 прямую O_1L, параллельную AC.

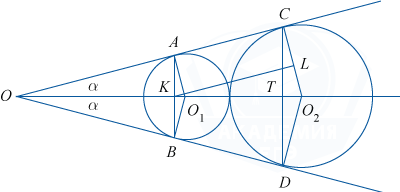
Тогда по свойству соответственных углов при параллельных прямых OC и O_1L и секущей OO_2\enspace \angle LO_1O_2=\alpha. Но O_1O_2=2+6=8, а LO_2=6-2=4. Поэтому \sin \alpha =\frac{LO_2}{O_1O_2}=\frac48=\frac12. Так как \alpha — острый угол, то \alpha =30^{\circ} , \cos \alpha =\frac{\sqrt 3}2, tg \alpha =\frac1{\sqrt 3}.

Заметим, что \frac{AO_1}{OA} =tg \alpha =\frac{1}{\sqrt 3}, OA=\frac{AO_1}{tg\alpha }=\frac2{\dfrac{1}{\sqrt 3}}=2\sqrt 3.

OK=OA\cdot \cos \alpha =2\sqrt 3\cdot \frac{\sqrt 3}2=3.

Аналогично OC =\frac{CO_2}{tg\alpha }=\frac6{\dfrac{1}{\sqrt 3}}=6\sqrt 3.

В \triangle KOC по теореме косинусов KC^2= OK^2 +OC^2 -2\cdot OK\cdot OC\cdot \cos \alpha = 9+108-2\cdot 3\cdot 6\sqrt 3\cdot \frac{\sqrt 3}2= 63,  KC=\sqrt {63}=3\sqrt 7.

3\sqrt 7.

а) Чтобы доказать, что точки P, M, Q и K лежат на одной окружности, можно воспользоваться одним из признаков, например доказать, что \angle PMK=\angle PQK. Найдём эти углы.

M — центр окружности, описанной около треугольника NPK, тогда как центральный и вписанный углы, опирающиеся на одну дугу, \angle PMK=2\angle PNK.

Запишем сумму углов треугольника PMK и воспользуемся полученным и заданным в условии равенствами.

\angle PMK+\angle MPK+\angle MKP= 2\angle PNK+\angle PNK= 3\angle PNK= 180^{\circ},

\angle PNK=60^{\circ}; \angle PMK=120^{\circ}.

Q — центр вписанной в треугольник NPK окружности, поэтому Q — точка пересечения биссектрис треугольника.

\angle PQK= 180^{\circ}-(\angle QPK+\angle QKP)= 180^{\circ}-\frac{\angle NPK+\angle NKP}2.

\angle PQK= 180^{\circ}-\frac{180^{\circ}-\angle PNK}2= 180^{\circ}-\frac{180^{\circ}-60^{\circ}}2= 120^{\circ}.

Значит, \angle PMK=\angle PQK, поэтому точки P, M, Q и K лежат на одной окружности.

б) W — точка пересечения высот треугольника NPK. Найдём угол MQW, для этого

докажем сначала, что и точка W лежит на той же окружности, что и точки P, M, Q и K. Если провести высоту треугольника (например, из вершины P), то образуются прямоугольные треугольники, сумма острых углов каждого такого треугольника равна 90^{\circ}. Например, \angle WPK+\angle PKN=90^{\circ}, аналогично можно получить: \angle WKP+\angle NPK=90^{\circ}.

\angle PWK= 180^{\circ}-\angle WPK-\angle WKP= 180^{\circ}-(90^{\circ}-\angle PKN)-(90^{\circ}-\angle NPK)= \angle PKN+\angle NPK= 120^{\circ}, \angle PMK=\angle PQK=\angle PWK, потому точки P, M, Q, W и K лежат на одной окружности.

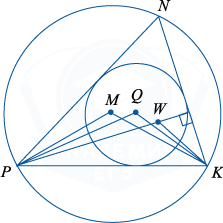
Так как \angle PNK=60^{\circ}, \angle NPK=47^{\circ}, получаем: \angle NKP=73^{\circ}. В равнобедренном треугольнике PMK, \angle MPK=\frac{180^{\circ}-\angle PMK}2=30^{\circ}. Учитывая, что PW \perp NK, получаем: \angle WPK=90^{\circ}-\angle NKP=17^{\circ}. Отсюда \angle WPM=\angle MPK-\angle WPK=13^{\circ}.

\angle MPK=30^{\circ}, \angle QPK=\frac{\angle NPK}2=\frac{47^{\circ}}2=23, 5^{\circ}

\angle KPW= 90^{\circ}-\angle NKP= 90^{\circ}-73^{\circ}= 17^{\circ}, значит, \angle MPK>\angle QPK>\angle KPW, поэтому лучи PW, PQ и PM пересекают дугу окружности в порядке, указанном на рисунке.

Четырёхугольник PMQW вписан в окружность, поэтому сумма его противоположных углов равна 180^{\circ} и \angle MQW= 180^{\circ}-\angle WPM= 180^{\circ}-13^{\circ}= 167^{\circ}.

б) 167^{\circ}.

а) \triangle ANO \sim \triangle BMO по первому признаку подобия (\angle ANO=\angle BMO=90^{\circ}, \angle AON=\angle BOM как вертикальные). Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим \frac{AO}{OB}=\frac{NF}{KM} (1).

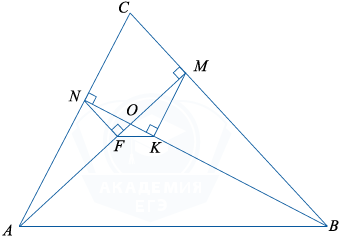
\triangle NFO \sim \triangle MKO по первому признаку подобия

(\angle NFO=\angle MKO=90^{\circ}, \angle NOF=\angle MOK как вертикальные), отсюда \frac{OF}{OK}=\frac{NF}{MK}. (2).

Из 1) и 2) следует, что \frac{AO}{OB}=\frac{OF}{OK}.

Следовательно, \triangle AOB \sim \triangle FOK по второму признаку подобия (\angle AOB — общий, \frac{AO}{FO}=\frac{OB}{OK}).

Из подобия следует \angle OAB=\angle OFK. Углы OAB и OFK соответственные при прямых AB и KF и секущей AO, следовательно, AB \parallel KF по признаку параллельности прямых.

б) В четырёхугольнике NCMO, \angle MON= 360^{\circ}-(\angle N+\angle M+\angle C)= 120^{\circ}.

В \triangle MOK, \angle MKO=90^{\circ}, \angle MOK=60^{\circ} как смежный с \angle MON, тогда \angle OMK=30^{\circ}. Пусть OK=x, OM=2OK=2x.

В \triangle OMB, \angle OMB=90^{\circ}, \angle MOB=60^{\circ}, \angle MBO=30^{\circ}, OB=2OM=4x.

По доказанному в пункте а) \triangle FOK \sim \triangle AOB, значит, сходственные стороны пропорциональны: \frac{KF}{AB}=\frac{OK}{OB}=\frac{x}{4x}=\frac14.

Следовательно, KF:AB=1:4.

KF:AB=1:4.

а) Пусть K и L — точки касания окружности и сторон BC и AC соответственно.

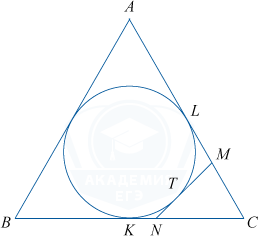
Так как MT=ML и NK=NT как отрезки касательных, проведенных из одной точки, то

P_{MNC}= CM+MT+TN+NC= CM+ML+KN+NC= CL+KC.

Так как ABC — правильный треугольник, то CL=KC=\frac{AC}{2}. Следовательно, P_{MNC}=AC, что и требовалось доказать.

б) 1. Обозначим TN=x, CM=a. Так как CM:MA=1:4 по условию, то MA=4a и AC=5a.

Тогда CL=\frac{AC}{2}=\frac{5}{2}a и ML=CL-CM=\frac{5}{2}a-a=\frac{3}{2}a. Так как ML=MT, то MT=\frac{3}{2}a. Тогда MN=MT+TN=\frac{3}{2}a+x.

Так как NT=NK, то NK=x. Тогда CN=CK-NK=\frac{BC}{2}-x=\frac{5}{2}a-x.

2. По теореме косинусов для треугольника MNC

MN^2=CN^2+CM^2- 2 \cdot CN \cdot CM \cdot \cos \angle NCM. Подставляя в это уравнение выражения для сторон треугольника MNC, получим:

\left ( \frac{3}{2}a+x\right )^2= \left ( \frac{5}{2}a-x\right )^2+a^2-2\left ( \frac{5}{2}a-x\right )a \cos 60^\circ;

\frac{9}{4}a^2+2 \cdot \frac{3}{2}ax+x^2= \frac{25}{4}a^2-2 \cdot \frac{5}{2}ax+x^2+a^2- 2\left ( \frac{5}{2}a-x \right )a \cdot \frac{1}{2};

7ax=\frac{5}{2}a^2;

x=\frac{5}{14}a.

Таким образом, TN=x=\frac{5}{14}a.

3. Тогда MT:TN=\frac{3}{2}a:\frac{5}{14}a=21:5.

б) 21:5.