Задание №1205

Тип задания: 16
Тема: Окружности и треугольники

Условие

Две окружности касаются внешним образом в точке P. Прямая MN касается первой окружности в точке M, а второй — в точке N.

а) Докажите, что \triangle MNP прямоугольный.

б) Найдите площадь \triangle MNP, если известно, что радиусы окружностей равны 4 и 16.

Показать решение

Решение

а) Пусть O_1 и O_2 — центры касающихся окружностей. Через точку P проведём общую касательную заданных окружностей и обозначим через Q точку пересечения этой касательной с прямой MN.

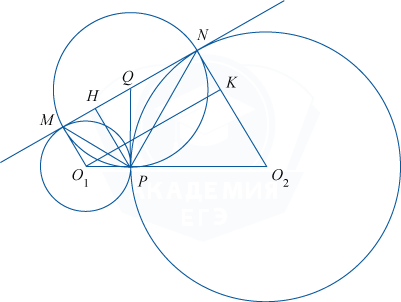
Две окружности, касающиеся внешним образом и образованный треугольник

По свойству касательных, проведённых к окружности, будем иметь: QM=QP, QN=QP. Значит, точки M, N и P равноудалены от точки Q, следовательно, \angle MPN является вписанным в некоторую окружность с центром в точке Q и радиусом R=MQ. При этом \angle MPN опирается на диаметр MN, а значит, \angle MPN=90^{\circ}. Отсюда \triangle MNP является прямоугольным.

б) Пусть O_1 — центр окружности радиуса 4, а O_2 — центр окружности радиуса 16.

Рассмотрим MNO_2O_1: прямая MN — касательная к исходным окружностям, O_1M и

O_2N — радиусы, следовательно, O_1M \perp MN и O_2N \perp MN. Отсюда O_1M \parallel O_2N, а значит MNO_2O_1 — прямоугольная трапеция.

Точка касания двух окружностей лежит на линии их центров, поэтому отрезок

O_1O_2 пересекает касательную PQ в точке P, следовательно, O_1P=O_1M=4, O_2P=O_2N=16, O_1O_2=O_1P+O_2P=4+16=20.

Проведём из точки P перпендикуляр PH к отрезку MN.

Очевидно, что S_{\triangle MPH}=S_{MNO_2O_1}-S_{\triangle MPO_1}-S_{\triangle MPO_2}.

Приведем отрезок O_1K\perp NO_2, K\in NO_2, получим прямоугольник MNKO_1, в котором MN=O_1K и KN=O_1M=4, а также прямоугольный \triangle O_1KO_2, в котором KO_2=NO_2-NK=16-4=12.

Следовательно, по теореме Пифагора O_1K= \sqrt {O_1O_2^2-KO_2^2}= \sqrt {20^2-12^2}= 16, MN-O_1K=16.

По теореме Фалеса \frac{MH}{MN}=\frac{O_1P}{O_1O_2}, следовательно, MH =\frac{MN\cdot O_1P}{O_1O_2}=\frac{16\cdot 4}{20}=\frac{16}5, отсюда NH=MN-MH=16-\frac{16}5=\frac{64}5.

S_{MNO_2O_1}= \frac{MO_1+NO_2}{2}\cdot MN= \frac{4+16}2\cdot 16= \frac{20}2\cdot 16= 160.

MH равна высоте треугольника MPO_1, опущенной на сторону MO_1.

S_{\triangle MPO_1}= \frac{MH\cdot MO_1}2 = \frac{\dfrac{16}5\cdot 4}{2}= 6,4.

NH равна высоте треугольника NPO_2, опущенной на сторону NO_2.

S_{\triangle MPO_2}= \frac{NH\cdot NO_2}2= \frac{\dfrac{64}5\cdot 16}{2}= 102,4.

Значит, S_{\triangle MPN}=160-6,4-102,4=51,2.