Задание №1001
Условие
К окружности, вписанной в правильный треугольник ABC, проведена касательная, пересекающая стороны AC и BC в точках M и N соответственно и касающаяся окружности в точке T.
а) Докажите, что периметр треугольника MNC равен стороне треугольника ABC.
б) Найдите MT:TN, если известно, что CM: MA=1:4.
Решение
а) Пусть K и L — точки касания окружности и сторон BC и AC соответственно.
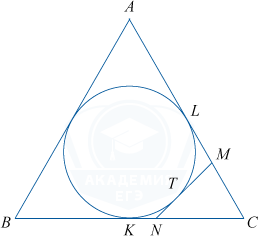
Так как MT=ML и NK=NT как отрезки касательных, проведенных из одной точки, то
P_{MNC}= CM+MT+TN+NC= CM+ML+KN+NC= CL+KC.
Так как ABC — правильный треугольник, то CL=KC=\frac{AC}{2}. Следовательно, P_{MNC}=AC, что и требовалось доказать.
б) 1. Обозначим TN=x, CM=a. Так как CM:MA=1:4 по условию, то MA=4a и AC=5a.
Тогда CL=\frac{AC}{2}=\frac{5}{2}a и ML=CL-CM=\frac{5}{2}a-a=\frac{3}{2}a. Так как ML=MT, то MT=\frac{3}{2}a. Тогда MN=MT+TN=\frac{3}{2}a+x.
Так как NT=NK, то NK=x. Тогда CN=CK-NK=\frac{BC}{2}-x=\frac{5}{2}a-x.
2. По теореме косинусов для треугольника MNC
MN^2=CN^2+CM^2- 2 \cdot CN \cdot CM \cdot \cos \angle NCM. Подставляя в это уравнение выражения для сторон треугольника MNC, получим:
\left ( \frac{3}{2}a+x\right )^2= \left ( \frac{5}{2}a-x\right )^2+a^2-2\left ( \frac{5}{2}a-x\right )a \cos 60^\circ;
\frac{9}{4}a^2+2 \cdot \frac{3}{2}ax+x^2= \frac{25}{4}a^2-2 \cdot \frac{5}{2}ax+x^2+a^2- 2\left ( \frac{5}{2}a-x \right )a \cdot \frac{1}{2};
7ax=\frac{5}{2}a^2;
x=\frac{5}{14}a.
Таким образом, TN=x=\frac{5}{14}a.
3. Тогда MT:TN=\frac{3}{2}a:\frac{5}{14}a=21:5.
Ответ
б) 21:5.