Задание №1000
Условие
Окружность касается сторон AB и BC треугольника ABC соответственно в точках D и E. Точки A, D, E и C лежат на одной окружности.
а) Докажите, что треугольник равнобедренный.
б) Найдите длину высоты треугольника ABC, опущенной из точки A, если длины сторон AB и AC соответственно равны 10 и 4.
Решение
а) Так как DB=BE по свойству касательных, проведённых к окружности из одной точки, то треугольник DBE — равнобедренный.
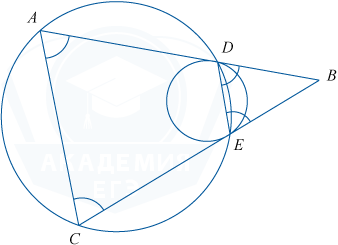
Значит, \angle BDE=\angle BED. Четырехугольник DACE вписан в окружность, поэтому \angle ACE+\angle ADE=180^\circ, откуда \angle ACB=180^{\circ}-\angle ADE=\angle BDE. Аналогично, \angle BAC=\angle DEB. Следовательно, треугольник ABC — равнобедренный и AB=BC.
б) Пусть длины высот треугольника ABC, опущенных из точек A и B соответственно, равны h_{a} и h_{b}.
Найдём h_b= \sqrt{AB^2-\left (\frac{AC}{2} \right )^2}= \sqrt{10^2-2^2}= 4\sqrt{6}. Площадь треугольника ABC равна \frac{1}{2}AC \cdot h_b=\frac{1}{2}BC \cdot h_a. Отсюда h_a=\frac{AC \cdot h_b}{BC}=\frac{4 \cdot 4\sqrt{6}}{10}=\frac{8\sqrt{6}}{5}.
Ответ
б) \frac{8\sqrt{6}}{5}.
Альберт Багов /