Задание №998
Условие
В окружность с центром O вписан остроугольный треугольник ABC, в котором проведена медиана AF, причём \angle FAC=\angle OCA.
а) Докажите, что точка O лежит на медиане AF.
б) Найдите площадь треугольника AOC, если \angle BAC=60^\circ, AB=12\sqrt{3}.
Решение
а) Докажем, что точка O лежит на медиане AF.
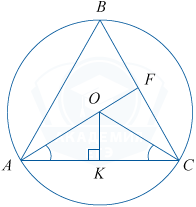
\bigtriangleup AOC — равнобедренный (AO=OC как радиусы), следовательно, \angle OAC=\angle OCA (как углы при основании равнобедренного треугольника). По условию \angle FAC=\angle OCA, значит, \angle FAC=\angle OAC.
\bigtriangleup ABC — остроугольный, значит, O лежит внутри треугольника, F и O лежат по одну сторону от AC. В этом случае из равенства \angle FAC и \angle OAC следует, что точка O лежит на медиане AF.
б) \bigtriangleup BOC — равнобедренный, так как OB=OC (как радиусы), OF — медиана, тогда OF — высота, отсюда AF — высота в \bigtriangleup ABC, которая является медианой, значит, \bigtriangleup ABC — равнобедренный и AB=AC. По условию \angle BAC=60^\circ, \angle ABC=\angle BCA=60^\circ, BC=AB.
\bigtriangleup ABC — равносторонний, AF=AB \sin 60^\circ=\frac{AB\sqrt{3}}{2}; O — центр описанной и вписанной окружностей. Тогда OK=OF, OF= \frac{1}{3}AF= \frac{1}{3} \cdot \frac{AB\sqrt{3}}{2}= \frac{AB\sqrt{3}}{6}= \frac{12 \cdot 3}{6}=6.
S_{AOC}=\frac{1}{2}AC \cdot OK=6\sqrt{3} \cdot 6=36\sqrt{3}.
Ответ
36\sqrt{3}