Задание №997
Условие
Окружность, вписанная в остроугольный треугольник ABC, касается сторон AB и AC в точках E и F.
а) Докажите, что центр окружности, вписанной в треугольник AEF, лежит на окружности, вписанной в треугольник ABC.
б) Найдите расстояние между центрами этих окружностей, если AB=11, AC=14, BK=3,08, где K — точка пересечения стороны BC и биссектрисы, проведённой из вершины A.
Решение
а) Пусть точка O — центр вписанной окружности треугольника ABC. O лежит на биссектрисе AK.
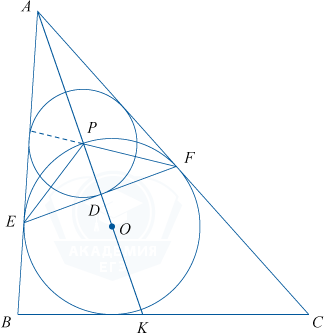
Биссектриса AK пересекает дугу EF в точке P, а отрезок EF — в точке D. AE=AF как отрезки касательных, проведенных к окружности из одной точки. Отсюда, \bigtriangleup EAF — равнобедренный, значит, биссектриса AD — медиана и высота. \bigtriangleup PDE=\bigtriangleup PDF по двум катетам (ED=DF, PD — общая сторона). Из равенства треугольников следует PE=PF, а так как равные хорды стягивают равные дуги, то \smile PE=\smile PF.
Докажем, что P — центр вписанной окружности треугольника EAF.
\angle AFP=\frac{1}{2} \smile PF как угол между касательной AF и хордой PF.
\angle EFP=\frac{1}{2} \smile PE как вписанный. Так как \smile PF=\smile PE, то \angle AFP=\angle EFP, значит, FP — биссектриса угла AFE.
Таким образом, P — точка пересечения биссектрис AD и FP треугольника AEF, следовательно, P — центр вписанной окружности.
б) По условию AK — биссектриса \bigtriangleup ABC, проведённая из вершины A. По свойству биссектрисы имеем \frac{BK}{AB}=\frac{CK}{AC},
CK=\frac{BK \cdot AC}{AB}=\frac{3,08 \cdot 14}{11}=3,92.
BC=BK+KC=3,08+3,92=7.
Пусть O — центр вписанной окружности в \bigtriangleup ABC, r — радиус этой окружности, p — полупериметр \bigtriangleup ABC.
p= \frac{AB+BC+AC}{2}= \frac{11+7+14}{2}= 16.
По формуле Герона S_{ABC}= \sqrt{p(p-AB)(p-BC)(p-AC)}= \sqrt{16 \cdot 5 \cdot 9 \cdot 2}= 12\sqrt{10},
r=\frac{S_{ABC}}{p}=\frac{12\sqrt{10}}{16}=\frac{3\sqrt{10}}{4}.
Расстояние между центрами окружностей OP=r=\frac{3\sqrt{10}}{4}.
Ответ
\frac{3\sqrt{10}}{4}