Задание №1208
Условие
Биссектриса острого угла параллелограмма пересекает его сторону в точке K. Окружность радиусом 3 проходит через точку пересечения диагоналей и касается трёх сторон параллелограмма, причём K — одна из точек касания.
а) Докажите, что треугольник ABK равнобедренный.
б) Найдите площадь параллелограмма.
Решение
а) По условию \angle BAK=\angle KAD, \angle KAD=\angle AKB как накрест лежащие при BC \parallel AD и секущей AK. Следовательно, \angle BAK=\angle AKB и \triangle ABK равнобедренный.
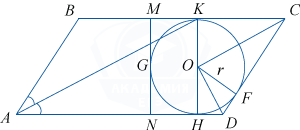
б) Пусть CF=x, FD=y, радиус окружности r, тогда, учитывая, что отрезки касательных, проведённых к окружности из одной точки, равны и треугольник ABK равнобедренный, найдём AD=2x+y, поэтому площадь параллелограмма равна S=2r(2x+y)=6(2x+y).
С другой стороны, площадь параллелограмма равна удвоенной площади прямоугольной трапеции CDNM, так как G — точка пересечения диагоналей, поэтому S= 2\cdot \frac12\cdot P_{CDNM}\cdot r= (4r+2x+2y)\cdot r= 2r(2r+x+y)= 6(6+x+y).
Приравнивая площади, получим уравнение 2x+y=6+x+y, откуда x=6.
\angle COD=90^{\circ} как угол, образованный двумя биссектрисами смежных углов. Из \triangle COD, OF^2=CF\cdot FD, r^2=x\cdot y, отсюда y=\frac{r^2}x=\frac96=\frac32.
Теперь найдём площадь параллелограмма ABCD, воспользовавшись одной из формул
S=6(2x+y)=6\left( 2\cdot 6+\frac32 \right) =81.
Ответ
81