Задание №181

Условие

Известно, что ABCDE — выпуклый пятиугольник.

а) Докажите, что сумма длин диагоналей пятиугольника меньше удвоенного периметра.

б) Найдите сумму длин диагоналей данного пятиугольника, если \bigtriangleup BED - равносторонний, AB=AE=BC=CD=\sqrt{3}, \angle BAE=\angle ABC=\angle BCD.

Показать решение

Решение

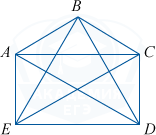Выпуклый пятиугольник а) Докажем, что сумма длин диагоналей пятиугольника меньше его удвоенного периметра.

Из неравенства треугольника следует, что AC<AB+BC, BD<BC+CD, CE<CD+DE, AD<AE+DE, BE<AB+AE.

Отсюда сумма диагоналей

AC+BD+CE+AD+BE < 2(AB+BC+CD+DE+AE).

б) По условию \bigtriangleup BED — равносторонний, AB=AE=BC=CD=\sqrt{3}, \angle BAE=\angle ABC=\angle BCD.

Тогда \angle BED=\angle BDE=\angle DBE=60^{\circ}. Пусть \angle AEB= \angle \alpha. Тогда \angle ABE=\alpha, так как \bigtriangleup ABE — равнобедренный. \angle EAB=180^{\circ}-2\alpha. Но \bigtriangleup AEB=\bigtriangleup ABC=\bigtriangleup BCD по двум сторнам и углу между ними. Таким образом, \angle CBD=\angle CDB=\alpha, \angle BCD=180^{\circ}-2\alpha. \angle ABC=2\alpha +60^{\circ}. Следовательно, 60^{\circ}+2\alpha=180^{\circ}-2\alpha, \alpha=30^{\circ}.

\angle AED=\angle CDE=\alpha+60^{\circ} \angle EAB= \angle ABC=\angle BCD=120^{\circ}, \angle AED=\angle CDE=\alpha +60^{\circ}=90^{\circ}. В \bigtriangleup BAE по теореме косинусов BE^2=AB^2+AE^2-2AB\cdot AE\cdot \cos \angle BAE= (\sqrt{3})^2+(\sqrt{3})^2-2\sqrt{3}\sqrt{3}\cos 120^{\circ}= 6+3=9, BE=3.

Значит, BE=AC=BD=3.

В \bigtriangleup CDE по теореме Пифагора CE^2=DE^2+CD^2=3^2+(\sqrt{3})^2=12, CE=2\sqrt{3}. Аналогично, AD=2\sqrt{3}. Сумма длин диагоналей равна 3+3+3+2\sqrt{3}+2\sqrt{3}=9+4\sqrt{3}.