Задания по теме «Неравенства»

1. Заметим, что x=0 решением системы не является, так как второе неравенство системы при x=0 не является верным (6 \leqslant 0). Пусть x>0.

Вычитая из первого неравенства второе, получаем

x^3-4x^2+x+6 \geqslant 0.

А вычитая из второго неравенства системы последнее неравенство, получаем

x^4-5x^3+5x^2+3x \leqslant 0,

x(x^3-5x^2+5x+3) \leqslant 0.

Так как x>0, то из последнего неравенства получаем:

x^3-5x^2+5x+3 \leqslant 0.

Таким образом система неравенств

\begin{cases} x^3-4x^2+x+6 \geqslant 0, \\ x^3-5x^2+5x+3 \leqslant 0 \end{cases}

является следствием исходной.

Вычитая из первого неравенства последней системы второе, умноженное на 2, и деля полученное неравенство на -x (причём снова обращаем внимание на известное нам ограничение x>0), получаем x^2-6x+9 \leqslant 0.

Последнее неравенство (следствие исходной системы) имеет единственное решение x=3. Простой подстановкой убеждаемся, что x=3 является решением системы.

3

ОДЗ неравенства: \begin{cases} x>0, \\ x\neq 1, \\ x\neq \frac14. \end{cases}

Т.к. \frac1{\log_x 0,5}= -\frac1{\log_x 2}= -\log_2 x, а \log_{4x} 2 =\frac1{\log_2 x+2}, то неравенство примет вид: -\log_2 x+6 \geqslant \frac{16}{\log_2 x+2}. Пусть \log_2 x=t, тогда \frac{16}{t+2}+ t-6 \leqslant 0, \frac{(t-2)^2}{t+2}\leqslant 0, t=2 или t<-2. \log_2 x=2, откуда x=4 или \log_2 x<-2, откуда x<\frac14. Учитывая ОДЗ, получим 0 < x < \frac14, x=4.

\left( 0;\,\frac14\right) , 4.

Заметим, что x>0, x \neq \frac12, x \neq 1.

Используя свойства логарифмов, преобразуем неравенство:

\frac1{\log_2x}+\frac2{\log_22x}\geqslant 2,

\frac1{\log_2x}+\frac2{\log_22+\log_2x}\geqslant 2,

\frac1{\log_2x}+\frac2{1+\log_2x}\geqslant 2.

Пусть \log_2x=t, тогда получим неравенство, которое удобно решить методом интервалов:

\frac1t+\frac2{1+t}\geqslant 2,

\frac{(1+t)+2t-2t(1+t)}{t(1+t)}\geqslant 0,

\frac{2t^3-t-1}{t(1+t)}\leqslant 0,

\frac{(2t+1)(t-1)}{t(t+1)}\leqslant 0.

Получим два двойных неравенства, решим их, возвращаясь к переменной x:

1. -1< t \leqslant -\frac12,

\log_2\frac12<\log_2x\leqslant \log_2\frac1{\sqrt 2},

\frac12<x\leqslant \frac1{\sqrt 2}.

2. 0<t\leqslant 1,

\log_21<\log_2x\leqslant \log_22,

1<x\leqslant 2.

Так как найденные значения переменной удовлетворяют ОДЗ, то решение неравенства — \left( \frac12; \frac1{\sqrt 2}\right] \cup (1; 2].

\left( \frac12; \frac1{\sqrt 2}\right] \cup (1; 2].

ОДЗ: 7-2^x>0, x<\log_27.

Заметим, что \sqrt 2>1,4, a \sqrt 3>1,7. Тогда \frac{\sqrt 2+\sqrt 3}3>1.

Получаем неравенство 5\geqslant 7-2^x, 2^x\geqslant 2, x\geqslant 1.

С учетом ОДЗ имеем x\in[1; \log_27).

[1; \log_27).

План решения.

1. Отдельно преобразуем числитель и знаменатель.

1.1. В числителе вынесем за скобки 5^x, чтобы в скобке осталась разность некоторого числа в степени x и константы (вместо этого можно вынести за скобки 3^x, а потом дополнительно преобразовать, или сразу вынести за скобки 3^{x+1}).

1.2. В знаменателе «избавимся» от \log_2 5 в показателе степени (преобразуем его в множитель). После этого получим квадратичное выражение от 2^x (если сделать замену t=2^x, то получим квадратичное выражение от t). Квадратичное выражение разложим на множители.

2. Все множители в числителе и знаменателе заменим более простыми, совпадающими по знаку (в том числе равными нулю одновременно с исходными — таким образом, не надо будет дополнительно думать об ОДЗ).

3. Решим неравенство, полученное на предыдущем шаге, методом интервалов.

Решение.

1. \frac{3^x-5^{x+1}}{4^x-2^{x+\log_25}+4}\leqslant 0,

\frac{\left( \left( \dfrac35\right) ^x-5\right)\cdot 5^x}{2^{2x}-5\cdot 2^x+4}\leqslant 0,

\frac{\left( \dfrac35\right) ^x-5}{(2^x-4)(2^x-1)}\leqslant 0.

2. \frac{\left( \dfrac35\right) ^x-\left( \dfrac35\right) ^{\log_\tfrac355}}{(2^x-2^2)(2^x-2^0)}\leqslant 0.

Выражения \left( \frac35\right) ^x-5, 2^x-2^2, 2^x-2^0 совпадают по знаку с выражениями \left( \frac35-1\right)\cdot {x-\log_{\tfrac35}5}, (2-1)\cdot (x-2) и (2-1)\cdot (x-0) соответственно.

\frac{\left( \dfrac35-1\right)\cdot (x-\log_{\tfrac35}5)}{(2-1)\cdot (x-2)\cdot (2-1)\cdot (x-0)}\leqslant 0.

3. \frac{x-\log_{\tfrac35}5}{(x-2)\cdot x}\geqslant 0.

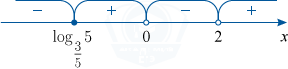
x\in[\log_{\tfrac35}5; 0)\cup (2; +\infty ).

[\log_{\tfrac35}5; 0)\cup(2; +\infty ).

3^{2x^2+7}+3^{x^2+4x+3}-4\cdot 3^{8x}\geqslant 0, разделим обе части неравенства на 3^{8x}\neq 0, 3^{8x}>0; неравенство примет вид 3^{2x^2-8x+7}+3^{x^2-4x+3}\geqslant 0, введем обозначение 3^{x^2-4x+3}=t, t>0, получим: 3t^2+t-4\geqslant 0. Найдем корни уравнения 3t^2+t-4=0,  t_1=-\frac43,  t_2=1. Решением неравенства 3t^2+t-4\geqslant0 являются промежутки \left( -\infty ; -\frac43\right] и \left[ 1; +\infty \right). Так как t>0, то 3^{x^2-4x+3}\geqslant 1, 3^{x^2-4x+3}\geqslant 3^0, x^2-4x+3\geqslant 0, x\leqslant 1 и x\geqslant 3. То есть решениями этого неравенства являются x\in(-\infty ; 1]\cup [3;+\infty ).

(-\infty ; 1]\cup [3;+\infty ).

3^{3x}-3^x\cdot 2^{2x}\cdot 3+3^{2x}\cdot 2^x-3\cdot 2^{3x} \geqslant 0.

Разделим обе части неравенства на 2^{3x}, 2^{3x} \neq 0, 2^{3x}>0, неравенство примет вид \frac{3^{3x}}{2^{3x}}-\frac{3^x\cdot 2^{2x}\cdot 3}{2^{3x}}\,\,\,+ \frac{3^{2x}\cdot 2^x}{2^{3x}}-\frac{3\cdot 2^{3x}}{2^{3x}}\geqslant 0,

\left( \frac32\right) ^{3x}-3\cdot \left( \frac32\right) ^x+\left( \frac32\right) ^{2x}-3\geqslant 0, введем обозначение \left( \frac32\right) ^x=t, t>0.

t^3+t^2-3t-3\geqslant 0,

t^2(t+1)-3(t+1)\geqslant 0,

(t+1)(t^2-3)\geqslant 0,

t\in[-\sqrt 3;-1]\cup [\sqrt 3;+\infty ), но t>0, следовательно, решением неравенства t^3+t^2-3t-3\geqslant 0 является t\in[\sqrt 3;+\infty ).

\left( \frac32\right) ^x=t, тогда \left( \frac32\right) ^x\geqslant \sqrt 3.

x\geqslant \log_{\tfrac32}\sqrt 3=\frac{\dfrac12\log_33}{\log_33-\log_32},

x\geqslant \frac1{2(1-\log_32)}.

x \in\left[ \frac1{2(1-\log_32) }; +\infty \right).

\left[ \frac1{2(1-\log_32) }; +\infty \right).

ОДЗ неравенства является множество всех решений системы

\begin{cases} x^2+x>0,\\ x^2+x\neq 1; \end{cases} \begin{cases} x^2+x>0,\\ x^2+x-1\neq 0.\end{cases}

x \in \left( -\infty ; \frac{-1-\sqrt 5}{2}\right)\,\, \cup \left( \frac{-1-\sqrt 5}{2}; -1\right) \,\,\cup \left( 0;\frac{-1+\sqrt 5}{2}\right) \,\,\cup \left( \frac{-1+\sqrt 5}{2};+\infty \right).

Перейдём в неравенстве к логарифмам по основанию 2.

\frac1{\dfrac{\log_2 0,5}{\log_2(x^2+x)}}\,\,+ \frac1{\dfrac{\log_2 0,25}{\log_2(x^2+x)}}\,\,+ \frac1{ \dfrac{\log_2 4}{\log_2(x^2+x)}}\geqslant 1,

\frac{\log_2(x^2+x)}{-1}\,\,+ \frac{\log_2(x^2+x)}{-2}\,\,+ \frac{\log_2(x^2+x)}{2}\geqslant 1,

\log_2(x^2+x)\cdot \left( -1-\frac12+\frac12\right) \geqslant 1,

-\log_2(x^2+x)\geqslant 1,

\log_2(x^2+x)\leqslant 1.

\log_2(x^2+x)\leqslant \log_2 0,5,

x^2+x\leqslant 0,5,

x^2+x-0,5\leqslant 0.

Находим корни квадратного трёхчлена x^2+x-0,5:

x_{1,2}=\frac{-1\pm\sqrt 3}2, поэтому множеством решений неравенства x^2+x-0,5 \leqslant 0 будет множество \left[ \frac{-1-\sqrt 3}{2}; \frac{-1+\sqrt 3}{2}\right].

Так как \frac{-1-\sqrt 5}2<\frac{-1-\sqrt 3}2<-1 и 0<\frac{-1+\sqrt 3}2<\frac{-1+\sqrt 5}2, то множеством решений неравенства будет множество \left[ \frac{-1-\sqrt 3}2; -1\right) \cup \left( 0;\frac{-1+\sqrt 3}2\right].

\left[ \frac{-1-\sqrt 3}2; -1\right) \cup \left( 0;\frac{-1+\sqrt 3}2\right].

ОДЗ: \begin{cases} x+0,5>0,\\5^{1-\sqrt x}-1\neq 0,\\x\geqslant 0; \end{cases} \begin{cases} x\geqslant 0,\\x\neq 1. \end{cases}

x\in[0; 1) \cup (1; +\infty).

\frac{4 \log_2(x+0,5)-5^{\sqrt x} \log_2(x+0,5)\cdot (5^{1-\sqrt x}-1)}{5^{1-\sqrt x}-1}\leqslant 0,

\frac{\log_2(x+0,5)(4-5^{\sqrt {x}+1-\sqrt x}+5^{\sqrt x})}{5^{1-\sqrt x}-1}\leqslant 0.

\frac{\log_2(x+0,5)(5^{\sqrt x}-5^0)}{5^{1-\sqrt x}-5^0}\leqslant 0.

Применим метод замены множителя, учитывая, что:

а) \log_{h(x)}f(x)\rightarrow (h(x)-1)(f(x)-1), тогда \log_2(x+0,5)\rightarrow (2-1)(x+0,5-1)=x-0,5.

б) h(x)^{p(x)}-h(x)^{q(x)}\rightarrow (h(x)-1)(p(x)-q(x)),

тогда 5^{\sqrt x}-5^0=(5-1)(\sqrt x-0)=4\sqrt x,

5^{1-\sqrt x}-5^0= (5-1)(1-\sqrt x-0)= 4(1-\sqrt x).

Неравенство примет вид \frac{(x-0,5)\cdot \sqrt x}{1-\sqrt x}\leqslant 0.

На ОДЗ имеем 0 \leqslant x \leqslant 0,5; x>1.

[0; 0,5] \cup (1; +\infty ).

Найдём ОДЗ неравенства.

\begin{cases} 2-x > 0, \\ x > 0, \\ \log_{35}x^3-3\log_{49}x \neq 0;\end{cases}

\begin{cases}x < 2, \\ x > 0, \\ \frac{3 \ln x}{\ln 35} -\frac{3 \ln x}{\ln 49} \neq 0;\end{cases}

\begin{cases} x < 2, \\ x > 0, \\ \ln x \left ( \frac{1}{ \ln 35}-\frac{1}{\ln 49}\right ) \neq 0;\end{cases}

\begin{cases}x < 2, \\ x > 0, \\ \ln x \neq 0; \end{cases}

\begin{cases}x < 2, \\ x > 0, \\ x \neq 1; \end{cases}

(0;1) \cup (1;2).

Исследуем знак левой части неравенства.

При 0 < x < 1:

\log_{35}x^3-3\log_{49}x= 3\log_{35}x-3\log_{49}x= \frac{3}{\log_{x}35}-\frac{3}{\log_{x}49} < 0

(так как \log_{x}49 < \log_{x}35 < 0).

\log_{25}(2-x)+\log_{35}\left ( \frac{1}{2-x}\right )= \log_{25}(2-x)-\log_{35}(2-x)= \frac{1}{\log_{2-x}25}-\frac{1}{\log_{2-x}35} > 0 (так как 2-x > 1, и значит, 0 < \log_{2-x}25 < \log_{2-x}35).

При 1 < x < 2:

\log_{35}x^{3}-3 \log_{49}x= 3 \log_{35}x-3 \log_{49}x= \frac{3}{\log_{x}35}-\frac{3}{\log_{x}49} > 0

(так как 0 < \log_{x}35 < \log_{x}49);

\log_{25}(2-x)+\log_{35}\left ( \frac{1}{2-x}\right )= \log_{25}(2-x)-\log_{35}(2-x)= \frac{1}{\log_{2-x}25}-\frac{1}{\log_{2-x}35} < 0 (так как 2-x < 1, и значит, \log_{2-x}35 < \log_{2-x}25 < 0).

Таким образом, левая часть исходного неравенства отрицательна при всех значениях x из ОДЗ. С другой стороны, \log_{49}25 > 0. Значит, левая часть исходного неравенства не превосходит \log_{49}25 при любом значении x из ОДЗ.

Следовательно, решение данного неравенства: (0;1) \cup (1;2).

(0;1) \cup (1;2).