Задания по теме «Комбинированные неравенства»

План решения.

1. Отдельно преобразуем числитель и знаменатель.

1.1. В числителе вынесем за скобки 5^x, чтобы в скобке осталась разность некоторого числа в степени x и константы (вместо этого можно вынести за скобки 3^x, а потом дополнительно преобразовать, или сразу вынести за скобки 3^{x+1}).

1.2. В знаменателе «избавимся» от \log_2 5 в показателе степени (преобразуем его в множитель). После этого получим квадратичное выражение от 2^x (если сделать замену t=2^x, то получим квадратичное выражение от t). Квадратичное выражение разложим на множители.

2. Все множители в числителе и знаменателе заменим более простыми, совпадающими по знаку (в том числе равными нулю одновременно с исходными — таким образом, не надо будет дополнительно думать об ОДЗ).

3. Решим неравенство, полученное на предыдущем шаге, методом интервалов.

Решение.

1. \frac{3^x-5^{x+1}}{4^x-2^{x+\log_25}+4}\leqslant 0,

\frac{\left( \left( \dfrac35\right) ^x-5\right)\cdot 5^x}{2^{2x}-5\cdot 2^x+4}\leqslant 0,

\frac{\left( \dfrac35\right) ^x-5}{(2^x-4)(2^x-1)}\leqslant 0.

2. \frac{\left( \dfrac35\right) ^x-\left( \dfrac35\right) ^{\log_\tfrac355}}{(2^x-2^2)(2^x-2^0)}\leqslant 0.

Выражения \left( \frac35\right) ^x-5, 2^x-2^2, 2^x-2^0 совпадают по знаку с выражениями \left( \frac35-1\right)\cdot {x-\log_{\tfrac35}5}, (2-1)\cdot (x-2) и (2-1)\cdot (x-0) соответственно.

\frac{\left( \dfrac35-1\right)\cdot (x-\log_{\tfrac35}5)}{(2-1)\cdot (x-2)\cdot (2-1)\cdot (x-0)}\leqslant 0.

3. \frac{x-\log_{\tfrac35}5}{(x-2)\cdot x}\geqslant 0.

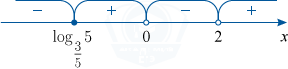
x\in[\log_{\tfrac35}5; 0)\cup (2; +\infty ).

[\log_{\tfrac35}5; 0)\cup(2; +\infty ).

ОДЗ: \begin{cases} x+0,5>0,\\5^{1-\sqrt x}-1\neq 0,\\x\geqslant 0; \end{cases} \begin{cases} x\geqslant 0,\\x\neq 1. \end{cases}

x\in[0; 1) \cup (1; +\infty).

\frac{4 \log_2(x+0,5)-5^{\sqrt x} \log_2(x+0,5)\cdot (5^{1-\sqrt x}-1)}{5^{1-\sqrt x}-1}\leqslant 0,

\frac{\log_2(x+0,5)(4-5^{\sqrt {x}+1-\sqrt x}+5^{\sqrt x})}{5^{1-\sqrt x}-1}\leqslant 0.

\frac{\log_2(x+0,5)(5^{\sqrt x}-5^0)}{5^{1-\sqrt x}-5^0}\leqslant 0.

Применим метод замены множителя, учитывая, что:

а) \log_{h(x)}f(x)\rightarrow (h(x)-1)(f(x)-1), тогда \log_2(x+0,5)\rightarrow (2-1)(x+0,5-1)=x-0,5.

б) h(x)^{p(x)}-h(x)^{q(x)}\rightarrow (h(x)-1)(p(x)-q(x)),

тогда 5^{\sqrt x}-5^0=(5-1)(\sqrt x-0)=4\sqrt x,

5^{1-\sqrt x}-5^0= (5-1)(1-\sqrt x-0)= 4(1-\sqrt x).

Неравенство примет вид \frac{(x-0,5)\cdot \sqrt x}{1-\sqrt x}\leqslant 0.

На ОДЗ имеем 0 \leqslant x \leqslant 0,5; x>1.

[0; 0,5] \cup (1; +\infty ).

Найдём область определения неравенства.

\begin{cases}x+4 >0, \\5^{x^{2}+1}-5^{x} \neq0; \end{cases}

\begin{cases} x > -4, \\ x^{2}+1 \neq x;\end{cases}

\begin{cases} x > -4, \\ x^{2}-x+1 \neq 0;\end{cases}

x > -4.

Для решения данного неравенства применяем метод интервалов.

а) Пусть f(x)= \frac{(|2x+1|-x-2) \cdot \left ( \log_{\tfrac{1}{3}}(x+4)+1 \right )}{5^{x^{2}+1}-5^{x}}.

б) Область определения функции f(x): D(f)=(-4;+\infty ).

в) Нули функции f(x): f(x)=0.

\frac{(|2x+1|-x-2) \cdot \left ( \log_{\tfrac{1}{3}}(x+4)+1 \right )}{5^{x^{2}+1}-5^{x}}=0\Leftrightarrow

\Leftrightarrow \begin{cases} (|2x+1|-x-2) \cdot \left ( \log_{\tfrac{1}{3}}(x+4)+1 \right )=0, \\ x >-4; \end{cases}

\begin{cases} \left[\!\!\begin{array}{l} |2x+1|-x-2=0, \\ \log_{\tfrac{1}{3}}(x+4)+1=0 \end{array}\right. \\x > -4. \end{cases}

Уравнение |2x+1|-x-2=0 или |2x+1|=x+2 равносильно системе

\begin{cases} (2x+1)^2=(x+2)^2,\\x+2 \geq 0; \end{cases} \Leftrightarrow \begin{cases}\left[\!\!\begin{array}{l}x=-1,\\x=1,\end{array}\right.\\ x+2 \geq 0;\end{cases} \Leftrightarrow x=\pm 1.

Уравнение \log_{\tfrac{1}{3}}(x+4)+1=0 имеет корень x=-1.

г) Промежутки знакопостоянства функции f(x). На каждом из промежутков (-4;-1), (-1;1), (1; +\infty ) функция f(x) непрерывна и сохраняет постоянный знак. Так как f(-2) > 0, f(0) > 0, f(2) < 0, то f(x) \geq 0 при всех значениях x \in (-4;1].

(-4;1].

Данное неравенство равносильно неравенству (3^{x}-27)\sqrt{5x-x^{2}+14} \leq 0. Будем использовать метод интервалов, предварительно найдя ОДЗ и нули левой части неравенства.

Найдём ОДЗ неравенства:

-x^{2}+5x+14 \geq 0,  x^{2}-5x-14 \leq 0,  (x-7)(x+2) \leq 0,  x \in [-2;7].

Найдём нули левой части неравенства: (3^{x}-27)\sqrt{5x-x^{2}+14}=0,

3^{x}-27=0,  3^{x}=3^{3},  x=3.

\sqrt{5x-x^{2}+14}=0,  -x^{2}+5x+14=0,  x_{1}=-2,  x_{2}=7.

Найдем знаки выражения (3^{x}-27)\sqrt{5x-x^{2}+14}

x \in [-2;3] \cup \{7\}.

[-2;3]\cup\{7\}

ОДЗ: \begin{cases} x+5 > 0,\\2^{x+2}-4^x-3 \neq 0;\end{cases}\enspace \begin{cases} x> -5, \\ 2^{2x} -4 \cdot 2^x+3 \neq0;\end{cases}\enspace \begin{cases} x > -5, \\ x\neq 0, \\ x \neq \log_2 3\end{cases}.

x \in(-5;0)\cup(0;\log_2 3)\cup (\log_2 3; +\infty ).

\frac{(1-4\cdot2^x+4^x+3)\log_2 (x+5)}{(2^x -1)(2^x -3)} \geq0,

\frac{(2^x -2)^2 \log_2 (x+5)}{(2^x - 2^0)(2^x -2^{\log_2 3})} \geq0.

Применим метод замены множителя, учитывая, что

а) \log_{h(x)} f(x)\rightarrow (h(x)-1)(f(x)-1), тогда

\log_2 (x+5) \rightarrow (2-1)(x+5-1)= x+4.

б) h(x)^{p(x)}-h(x)^{q(x)} \rightarrow (h(x)-1) (p(x)-q(x)), тогда

2^x -2\rightarrow (2-1)(x-1)=x-1,

2^x -2^0 =(2-1)(x-0)=x ,

2^x -2^{\log_2 3}= (2-1)(x-\log_2 3)= x-\log_2 3.

Неравенство примет вид \frac{(x+4)(x-1)^2}{x(x-\log_2 3)} \geq 0. Решим его методом интервалов.

Учитывая ОДЗ x> -5, x \neq 0 и x\neq \log_2 3, получим -4 \leq x < 0; x > \log_2 3. x=1.

[-4;0)\cup\left\{1\right\}\cup(\log_2 3;+\infty)

Очевидно, что x > 0. Заметим, что \log_{2}x < 2^{x} при x > 0, график функции y=\log_{2}x лежит ниже прямой y=x, а график функции y=2^{x} лежит выше этой прямой, поэтому знаменатель дроби принимает только отрицательные значения. Докажем, что это верно.

Докажем, что 2^{x} > x. Рассмотрим f(x)=2^{x}-x.

f'(x)=2^{x} \ln2-1.

f'(x)=0 при 2^{x} \ln2-1=0, 

2^{x}=\frac{1}{\ln2},

x_{1}=\log_{2} \frac{1}{\ln2} — точка минимума, f(x_{1}) — наименьшее значение f(x).

Докажем, что f(x_{1}) > 0.

\frac{1}{\ln2}-\log_{2}\frac{1}{\ln2} > 0;

\log_{2}e-\log_{2}\log_{2}e > 0;

\log_{2}e > \log_{2}\log_{2}e;

e > \log_{2}e;

2^{e} > e.

Это верно, так как 2^{e} > 2^{2} > e.

Мы доказали, что 2^{x} > x. Но тогда \log_{2}2^{x} > \log_{2}x и x > \log_{2}x.

2^{x} > x > \log_{2}x, значит, 2^{x}-\log_{2}x > 0.

Умножив обе части неравенства на \log_{2}x-2^{x}, получим неравенство 4^{x}+\log_{2}x-12 \leq \log_{2}x-2^{x}, которое легко сводится к неравенству 4^{x}+2^{x}-12 \leq 0. Решив его методом подстановки, найдем все его решения x \leq \log_{2}3. Учитывая, что x > 0, получим все решения данного неравенства: x \in (0; \log_{2}3]

(0; \log_{2}3]

ОДЗ:

\begin{cases}x>0, \\ x-1>0, \\ x-1\neq1, \\ x^2+x\geqslant0, \\ x^2+x \neq x^2+5, \\ |x+2|\neq |x|; \end{cases} \begin{cases}x>0, \\ x>1, \\ x\neq2, \\\left[\!\!\begin{array}{l} x\geqslant 0, \\ x\leqslant -1, \end{array}\right. \\ x \neq 5, \\ x^2+4x+4\neq x^2; \end{cases} \begin{cases} x>1, \\ x\neq2, \\ x\neq 5.\end{cases}

x\in (1;2)\cup (2;5)\cup (5;+\infty ).

На ОДЗ данное неравенство равносильно неравенству

\frac{(x-3)(x-1-1)(x-3)}{(x^2+x-x^2-5)((x+2)^2-x^2)}\geqslant0,

\frac{(x-3)^2(x-2)}{(x-5)(4x+4)}\geqslant0,

\frac{(x-3)^2(x-2)}{(x-5)(x+1)}\geqslant0,

x\in (1;2]\cup \left \{ 3 \right \}\cup (5;+\infty ).

Учитывая ОДЗ, получим x\in (1;2)\cup \left \{ 3 \right \}\cup (5;+\infty ).

(1;2)\cup \left \{ 3 \right \}\cup (5;+\infty ).

ОДЗ:\enspace\begin{cases}2x+1\neq0,\\-x>0,\\ x+2>0; \end{cases}\enspace\begin{cases} x\neq\frac{1}{2},\\ x<0; \\ x>-2.\end{cases}

-2<x<-\frac{1}{2}, -\frac{1}{2}<x<0. Данное неравенство для всех x из ОДЗ равносильно неравенству \log_2\frac{x+2}{4}>-\frac{3}{2x+1}.

Решим последнее неравенство на каждом из промежутков ОДЗ.

1) -2<x<-\frac{1}{2}. Оценим левую и правую части неравенства:

\log_2\frac{x+2}{4}<\log_2\frac{3}{8}<0, -\frac{3}{2x+1}>0.

Так как для всех x из промежутка \left(-2;-\frac{1}{2}\right) выполняется неравенство \log_2\frac{x+2}{4}<0<-\frac{3}{2x+1}, то неравенство \log_2\frac{x+2}{4}>-\frac{3}{2x+1}, а следовательно, и исходное неравенство на промежутке \left(-2;-\frac{1}{2}\right) не имеет решений.

2) Если -\frac{1}{2}<x<0, то выполняется неравенства

\log_2\frac{x+2}{4}>\log_2\frac{3}{8}>\log_2\frac{1}{4}>-2.

-\frac{3}{2x+1}<-3, так как 0<2x+1<1. Значит, любое значение из промежутка \left(-\frac{1}{2};0\right) является решением неравенства \log_2\frac{x+2}{4}>-\frac{3}{2x+1}, а следовательно, и исходного неравенства.

Итак, множеством решений исходного неравенства является промежуток \left(-\frac{1}{2};0\right).

\left(-\frac{1}{2};0\right)

Преобразуем неравенство:

\ln \left ( 7^{\ln \left ( x^{2}-2x \right )} \right )\leq \ln \left ( \left ( 2-x \right )^{\ln 7} \right )

\ln 7\cdot \ln \left ( x^{2}-2x \right )\leq \ln7\cdot \ln\left ( 2-x \right )

\ln\left ( x^{2}-2x \right )\leq \ln\left ( 2-x \right )

0< x^{2}-2x\leq 2-x

\begin{cases} x^{2}-2x> 0 \\ \left ( x-2 \right )\left ( x+1 \right )\leq 0 \end{cases}

Получим -1\leq x< 0.

[-1; 0).