Задание №1194

План решения.

1. Отдельно преобразуем числитель и знаменатель.

1.1. В числителе вынесем за скобки 5^x, чтобы в скобке осталась разность некоторого числа в степени x и константы (вместо этого можно вынести за скобки 3^x, а потом дополнительно преобразовать, или сразу вынести за скобки 3^{x+1}).

1.2. В знаменателе «избавимся» от \log_2 5 в показателе степени (преобразуем его в множитель). После этого получим квадратичное выражение от 2^x (если сделать замену t=2^x, то получим квадратичное выражение от t). Квадратичное выражение разложим на множители.

2. Все множители в числителе и знаменателе заменим более простыми, совпадающими по знаку (в том числе равными нулю одновременно с исходными — таким образом, не надо будет дополнительно думать об ОДЗ).

3. Решим неравенство, полученное на предыдущем шаге, методом интервалов.

Решение.

1. \frac{3^x-5^{x+1}}{4^x-2^{x+\log_25}+4}\leqslant 0,

\frac{\left( \left( \dfrac35\right) ^x-5\right)\cdot 5^x}{2^{2x}-5\cdot 2^x+4}\leqslant 0,

\frac{\left( \dfrac35\right) ^x-5}{(2^x-4)(2^x-1)}\leqslant 0.

2. \frac{\left( \dfrac35\right) ^x-\left( \dfrac35\right) ^{\log_\tfrac355}}{(2^x-2^2)(2^x-2^0)}\leqslant 0.

Выражения \left( \frac35\right) ^x-5, 2^x-2^2, 2^x-2^0 совпадают по знаку с выражениями \left( \frac35-1\right)\cdot {x-\log_{\tfrac35}5}, (2-1)\cdot (x-2) и (2-1)\cdot (x-0) соответственно.

\frac{\left( \dfrac35-1\right)\cdot (x-\log_{\tfrac35}5)}{(2-1)\cdot (x-2)\cdot (2-1)\cdot (x-0)}\leqslant 0.

3. \frac{x-\log_{\tfrac35}5}{(x-2)\cdot x}\geqslant 0.

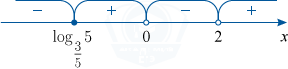
x\in[\log_{\tfrac35}5; 0)\cup (2; +\infty ).

[\log_{\tfrac35}5; 0)\cup(2; +\infty ).