Задание №1203
Условие
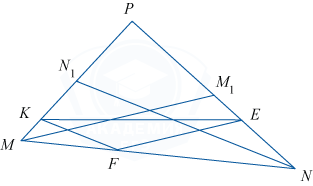
В треугольнике MNP проведены медианы MM_1 и NN_1. На сторонах MN, MP и NP взяты соответственно точки F, K и E, причём FE\parallel MM_1, FK\parallel NN_1 и MF:MN=1:3.
а) Докажите, что MK=\frac16MP, NE=\frac13PN.
б) Найдите площадь треугольника FEK, если площадь треугольника MNP равна 48.
Решение
а) Доказательство.
По условию MF:MN=1:3, то есть MF=\frac13MN.
По свойству параллельных линий, отсекающих пропорциональные отрезки на пересекаемых прямых, имеем MK =\frac13MN_1, MN_1=N_1P, значит, MN_1 =\frac12MP, MK =\frac16MP;
NE =\frac23NM_1, NM_1=M_1P, NE =\frac26PN =\frac13PN.
Что и требовалось доказать.
б) S_{FEK}= S_{MNP}-(S_{MKF}+S_{KPE}+S_{FEN}).
S_{MNP}=48; S_{MKF} = \frac12MK\cdot MF \sin \angle M= \frac12MP\cdot MN \sin \angle M\cdot \frac16\cdot \frac13= S_{MNP}\cdot \frac1{18}= 48\cdot \frac1{18} = \frac{24}9=\frac83.
S_{KPE}= \frac12KP\cdot PE \sin \angle P= \frac12MP\cdot PN \sin \angle P\cdot \frac56\cdot \frac23= S_{MNP}\cdot \frac{10}{18}= S_{MNP}\cdot \frac59= 48\cdot \frac59= \frac{80}3.
S_{FEN}= \frac12FN\cdot NE \sin \angle N= \frac12MN\cdot PN \sin \angle N\cdot \frac23\cdot \frac13= S_{MNP}\cdot \frac29= \frac{32}{3}.
S_{FEK}=48-\left( \frac83+\frac{80}3+\frac{32}3\right) =8.
Ответ
8