Задание №1202
Условие
Две окружности различных радиусов касаются друг друга внешним образом. Их общие касательные, не проходящие через точку касания окружностей, пересекаются в точке O. При этом одна из касательных касается окружностей в точках A и C, считая от точки O, а другая — соответственно в точках B и D.
а) Докажите, что прямая AB перпендикулярна биссектрисе угла, образованного указанными касательными.
б) Найдите расстояние от середины отрезка AB до точки C, если радиусы окружностей равны 2 и 6.
Решение
а) Рассмотрим рисунок.
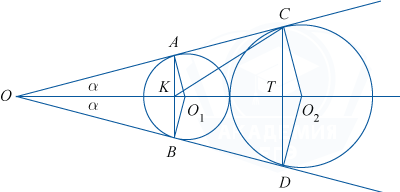
На нём O_1 и O_2 — центры окружностей (по свойству вписанной в угол окружности точки O_1 и O_2 лежат на биссектрисе \angle AOB), K и T — точки пересечения соответственно AB и CD с биссектрисой. O_1A и O_2C — радиусы окружностей, перпендикулярные касательной AC.
\triangle O_1AO=\triangle O_1BO по общей гипотенузе и острому углу, поэтому AO=BO. Таким образом, треугольник AOB является равнобедренным, и биссектриса OK угла O является высотой и медианой, поэтому точка K является серединой отрезка AB. Это и означает, что прямая AB перпендикулярна биссектрисе \angle AOB.
б) Пусть \angle AOO_1 равен \alpha. Проведём через O_1 прямую O_1L, параллельную AC.
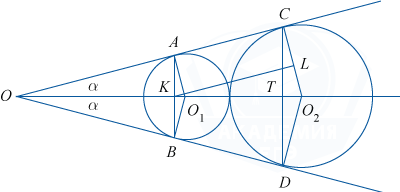
Тогда по свойству соответственных углов при параллельных прямых OC и O_1L и секущей OO_2\enspace \angle LO_1O_2=\alpha. Но O_1O_2=2+6=8, а LO_2=6-2=4. Поэтому \sin \alpha =\frac{LO_2}{O_1O_2}=\frac48=\frac12. Так как \alpha — острый угол, то \alpha =30^{\circ} , \cos \alpha =\frac{\sqrt 3}2, tg \alpha =\frac1{\sqrt 3}.
Заметим, что \frac{AO_1}{OA} =tg \alpha =\frac{1}{\sqrt 3}, OA=\frac{AO_1}{tg\alpha }=\frac2{\dfrac{1}{\sqrt 3}}=2\sqrt 3.
OK=OA\cdot \cos \alpha =2\sqrt 3\cdot \frac{\sqrt 3}2=3.
Аналогично OC =\frac{CO_2}{tg\alpha }=\frac6{\dfrac{1}{\sqrt 3}}=6\sqrt 3.
В \triangle KOC по теореме косинусов KC^2= OK^2 +OC^2 -2\cdot OK\cdot OC\cdot \cos \alpha = 9+108-2\cdot 3\cdot 6\sqrt 3\cdot \frac{\sqrt 3}2= 63, KC=\sqrt {63}=3\sqrt 7.
Ответ
3\sqrt 7.