Задание №1002
Условие
В прямоугольнике ABCD AB=24, AD=23. К окружности, радиус которой равен 12, с центром в точке A из точки C проведена касательная, которая пересекает сторону AD в точке M.
а) Докажите, что CM=2AM.
б) Найдите длину отрезка AM.
Решение
а) Используя условие задачи, выполним рисунок.
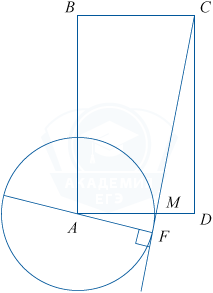
Проведём радиус AF в точку касания. AF \perp CF. \bigtriangleup AFM \sim \bigtriangleup MCD по двум углам (\angle AFM=\angle CDM=90^\circ, \angle AMF=\angle CMD как вертикальные).
AF:CD=12:24=1:2, откуда следует, что AM:MC=1:2, то есть MC=2AM.
б) Пусть AM=x, тогда CM=2x, MD=23-x. Для прямоугольного треугольника CDM справедлива теорема Пифагора:
CM^2=CD^2+MD^2, т.е. 4x^2=24^2+(23-x)^2,
3x^2+46x-1105=0.
Решая квадратное уравнение, получим x=13. Итак, AM=13.
Ответ
13
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Алексей Луговой /