Задание №999
Условие
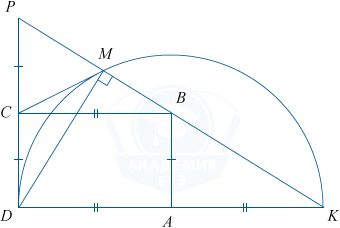
ABCD — прямоугольник. Окружность с центром в точке A радиуса AD пересекает продолжение стороны DA в точке K. Прямая KB пересекает прямую CD в точке P, а окружность во второй раз — в точке M.
а) Докажите, что CP=CM.
б) Найдите BD, если AM=15, MC=8.
Решение
а) Докажем, что DM \perp PK и CD=CP, а затем воспользуемся свойством медианы CM прямоугольного треугольника DPM. ABCD — прямоугольник, поэтому его углы прямые и CB=AD, CD=AB. \angle PCB=\angle BAK=90^\circ.
AD=AK как радиусы окружности. Получаем, что CB=AK. \angle PBC=\angle BKA как соответственные углы при CB \parallel AD (секущая PK).
\bigtriangleup PBC=\bigtriangleup BKA (по стороне и двум прилежащим к ней углам), значит, AB=CP. Но CD=AB, из этого получаем CD=CP.
\angle DMK — вписанный, он опирается на диаметр, значит, \angle DMK=90^\circ.
\angle PMD=180^\circ-\angle DMK=90^\circ. В прямоугольном треугольнике PDM медиана CM равна половине гипотенузы PD, значит, MC=CP=CD.
б) Воспользуемся теоремой Пифагора для треугольника BAD. BD^{2}=AD^{2}+AB^{2} (по теореме Пифагора). AM=AD (радиусы), AD=15. MC=CD=8 (см. пункт а). BD=\sqrt{15^{2}+8^{2}}=17.
Ответ
17