Задания по теме «Степенные функции»

ОДЗ: x \geqslant 0. Найдём производную исходной функции:

y'=8-\frac23\cdot\frac32x^\tfrac12=8-\sqrt x.

Вычислим нули производной:

8-\sqrt x=0;

\sqrt x=8;

x=64.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что точка x=64 является единственной точкой максимума заданной функции.

Найдём производную исходной функции, используя формулу производной произведения:

y'= \left((x+4)^2\right)'(x+1)+(x+4)^2(x+1)'= (19)'= 2(x+ 4)(x+1)+(x+4)^2= (x+4)(2x+2+x+4)= (x+4)(3x+6)= 3(x+4)(x+2).

Отыщем нули производной: y'(x)=0;

(x+4)(x+2)=0;

x_1=-4,  x_2=-2.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что на отрезке [-5; -4] исходная функция возрастает, а на отрезке [-4; -3] убывает. Таким образом, наибольшее значение на отрезке [-5; -3] достигается при x=-4 и равно y(-4)= (-4+4)^2(-4+1)+19= 19.

ОДЗ: x \geqslant 0. Найдём производную исходной функции:

y'=\frac23\cdot\frac32x^\tfrac12-5=\sqrt x-5.

Вычислим нули производной:

\sqrt x-5=0;

\sqrt x=5;

x=25.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что точка x=25 является единственной точкой минимума заданной функции.

Найдём производную исходной функции, используя формулу производной произведения:

y'= \left((x+9)^2\right)'(x+12)\,+ (x+9)^2(x+12)'-(14)'= 2(x+9)(x+12)+(x+9)^2= (x+9)(2x+24+x+9)= (x+9)(3x+33)= 3(x+9)(x+11).

Отыщем нули производной: y'(x)=0;

(x+9)(x+11)=0;

x_1=-11,  x_2=-9.

Расставим знаки производной и определим промежутки монотонности исходной функции на отрезке [-11; 3].

Из рисунка видно, что на отрезке [-11; -9] исходная функция убывает, а на отрезке [-9; 3] возрастает.

Таким образом, наименьшее значение на отрезке [-11; 3] достигается при x=-9 и равно y(-9)= (-9+9)^2(-9+12)-14= -14.

Найдём производную исходной функции, используя формулу производной произведения:

y'= \left((x-1)^2\right)'(x+8)\,\,+ (x-1)^2(x+8)'+(15)'= 2(x-1)(x+8)+(x-1)^2= (x-1)(2x+16+x-1)= (x-1)(3x+15)= 3(x-1)(x+5).

Отыщем нули производной: y'(x)=0;

(x-1)(x+5)=0;

x_1=1,  x_2=-5.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что x=1 является единственной точкой минимума.

Найдём производную исходной функции: y'(x)=24x^2+42x-90.

Найдём нули производной из уравнения y'(x)=0;

24x^2+42x-90=0;

4x^2+7x-15=0,

x_{1,2}= \frac{-7 \pm \sqrt{7^2-4\cdot4\cdot(-15)}}{2\cdot4}= \frac{-7\pm17}{8}.

Отсюда x_1=-3, x_2=\frac54. Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что функция y=8x^3+21x^2-90x-189 возрастает на промежутке [-5; -3] и убывает на промежутке [-3; 0,5]. Значит, на промежутке [-5; 0,5] наибольшее значение достигается при x=-3 и равно y(-3)= 8\cdot (-3)^3+21\cdot (-3)^2-90\cdot (-3)-189= -216+189+270-189=54.

Найдём производную исходной функции y'(x)=6x^2+18x-60.

Найдем нули производной из уравнения y'(x)=0,

6x^2+18x-60 = 0;

x^2 +3x-10 = 0,

x_{1,2} = \frac{-3\pm\sqrt{3^2-4\cdot1\cdot(-10)}}{2}= \frac{-3\pm7}{2}.

Отсюда x_1=-5,  x_2=2. Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что функция y=2x^3+9x^2-60x+5 убывает на промежутке [-1,5; 2] и возрастает на промежутке [2; 11]. Значит, на промежутке [-1,5; 11] наименьшее значение достигается при x=2 и равно y(2)= 2\cdot 2^3 +9\cdot 2^2 -60\cdot 2+5= 16+36-120+5= -63.

Найдём производную исходной функции: y'(x)=6x^2+72x+162.

Найдём нули производной из уравнения y'(x)=0;

6x^2+72x+162=0;

x^2+12x+27=0,

x_{1,2}=-6\pm \sqrt {6^2-1\cdot 27}=-6\pm 3.

Отсюда x_1=-9, x_2=-3. Расставим знаки производной и определим промежутки монотонности исходной функции.

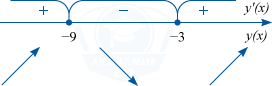
Из рисунка видно, что значение x=-3 является единственной точкой минимума.

Найдём производную исходной функции, используя формулу производной произведения:

y'= \left ( (x+7)^2 \right )'(x-6)+(x+7)^2(x-6)'+(11)'= 2(x+7)(x-6)+(x+7)^2= (x+7)(2x-12+x+7)= (x+7)(3x-5).

Отыщем нули производной:

y'(x)=0;

(x+7)(3x-5)=0,

x_1=-7,\,x_2=\frac53.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что x=-7 является единственной точкой максимума.

Найдём производную исходной функции: y'(x)=6x^2+80x+200.

Найдём нули производной из уравнения y'(x)=0;

6x^2+80x+200=0;

3x^2+40x+100=0,

x_{1,2}=\frac{-40\pm\sqrt{40^2-4\cdot3\cdot100}}{6}=\frac{-40\pm20}{6}. Отсюда x_1=-10, x_2=-\frac{10}{3}.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что значение x=-10 является единственной точкой максимума.