Задание №1110
Условие
Найдите точку минимума функции y=2x^3+36x^2+162x+57.
Решение
Найдём производную исходной функции: y'(x)=6x^2+72x+162.
Найдём нули производной из уравнения y'(x)=0;
6x^2+72x+162=0;
x^2+12x+27=0,
x_{1,2}=-6\pm \sqrt {6^2-1\cdot 27}=-6\pm 3.
Отсюда x_1=-9, x_2=-3. Расставим знаки производной и определим промежутки монотонности исходной функции.
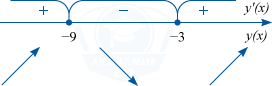
Из рисунка видно, что значение x=-3 является единственной точкой минимума.
Ответ
-3
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.