Задания по теме «Комбинации геометрических фигур»

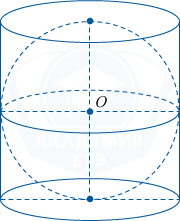
Из рисунка видно, что, с одной стороны, диаметр шара является диаметром окружности основания цилиндра, а с другой стороны, является высотой цилиндра. Пусть радиус шара равен R, тогда его диаметр равен 2R, значит, высота цилиндра H равна 2R. Находим объём цилиндра: V_цил. = S_осн. · H =\pi R^2 \cdot 2R = 2\pi R^3. По условию 66 = 2\pi R^3. Отсюда \pi R^3 = 33. Так как V_шара = R^3, то искомый объём равен \frac43\cdot33=44.

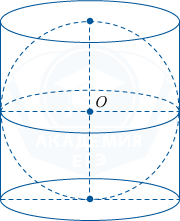
Из рисунка, указанного в условии, видно, что, с одной стороны, диаметр шара является диаметром окружности основания цилиндра, а с другой стороны, является высотой цилиндра. Пусть радиус шара равен R, тогда его диаметр равен 2R, значит, высота цилиндра H равна 2R. Находим площадь полной поверхности цилиндра: S _{полн. пов. цил.} = 2S _{осн. цил.} + S _{бок. пов. цил.} = 2\pi R^2 + 2\pi RH.

2\pi R^2 + 2\pi RH = 2\pi R^2 + 2\pi R\cdot 2R = 6\pi R^2. По условию 24 = 6\pi R^2. Отсюда \pi R^2 = 4. Так как S _{пов. шара} = 4\pi R^2, то искомая площадь равна 4\cdot 4 = 16.

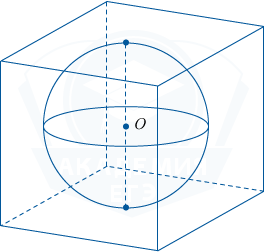
Пусть радиус шара равен R, тогда объём шара находится по формуле V = \frac43\pi R^3.

По условию 36\pi = \frac43\pi R^3. 108 = 4R^3, R^3 = 27, R = 3. Так как шар вписан в куб, то длина ребра куба равна длине диаметра шара, но диаметр шара в два раза больше радиуса и равен 3\cdot 2 = 6. Объём куба V находится по формуле V = a^3, где a — ребро куба. Поэтому V = a^3 = 6^3 = 216.

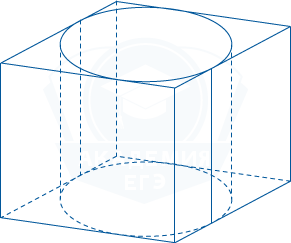
Основанием параллелепипеда является прямоугольник, описанный около окружности радиусом 5. Значит, этот прямоугольник является квадратом, сторона которого равна диаметру окружности основания цилиндра. Так как радиус r этой окружности равен 5, то диаметр равен двум радиусам, то есть 10. Объём параллелепипеда V находим по формуле V = S_осн · h = (2\cdot r)^2\cdot r, где h — высота параллелепипеда, которая равна высоте цилиндра, то есть равна 5. Значит, объем параллелепипеда V=10^2\cdot5=500.

Обозначим вершину конуса через A, а центр основания через O. Проведём через AO плоскость. В этой плоскости будет находиться диаметр сферы CB, AB — образующая конуса.

Тогда треугольник AOB — прямоугольный с прямым углом AOB. При этом AO=OB=R, где R — радиус сферы. По теореме Пифагора (AO)^2+(OB)^2=(AB)^2, R^2+R^2=(5\sqrt2)^2, 2R^2=25\cdot2, R^2=25, R=5.

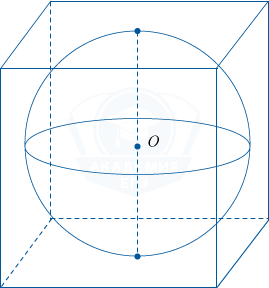
Так как куб описан около сферы, то длина диаметра этой сферы равна длине ребра куба. По условию радиус сферы равен 2, поэтому диаметр сферы в два раза больше и равен 4. Объём куба V находится по формуле V=a^3, где a — ребро куба. Поэтому V=a^3=4^3=64.

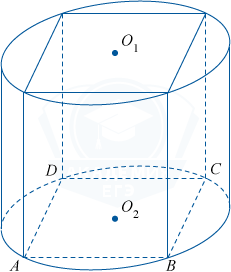
Рассмотрим рисунок, приведённый в условии. Диаметр основания цилиндра является диагональю AC квадрата ABCD, а радиус R основания цилиндра равен половине AC. Согласно теореме Пифагора AC= \sqrt{AB^2+BC^2}= \sqrt{4^2+4^2}= \sqrt{32}= 4\cdot\sqrt2. R=2\cdot\sqrt2. Заметим, что высота цилиндра совпадает с высотой призмы h. Отсюда следует, что V = S_осн. · h = \pi\cdot R^2\cdot h= \pi\cdot(2\sqrt2)^2\cdot\frac{4}{\pi}= 8\cdot4= 32.

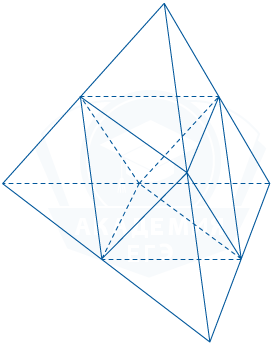
Площадь поверхности тетраэдра равна сумме площадей 4 одинаковых граней. Площадь грани равна \frac{46}{4}. Площадь поверхности многогранника равна сумме площадей 8 его граней, при этом каждая его грань — треугольник, образованный средними линиями грани тетраэдра, поэтому площадь этой грани равна \frac14 площади грани тетраэдра.

Искомая площадь равна \frac14\cdot\frac{46}{4}\cdot8=23.

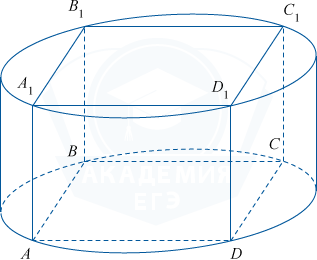
Радиус окружности, описанной вокруг квадрата со стороной 4, равен r=\frac{4}{\sqrt2}=2\sqrt2.

Объем цилиндра равен V= \pi r^2h= \pi\cdot(2\sqrt2)^2\cdot\frac{8}{\pi}= \pi\cdot8\cdot\frac{8}{\pi}= 64.

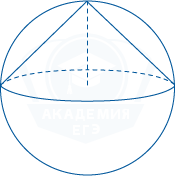
Так как центры сферы и основания конуса совпадают, то образующие конуса пересекаются под прямым углом. Найдем гипотенузу прямоугольного треугольника, катетами которого являются образующие конуса, а гипотенузой – диаметр сферы. Воспользуемся теоремой Пифагора:

d^2=2\cdot (7\sqrt{2})^2=2\cdot 2\cdot 7^2=2^2\cdot 7^2

d = 2\cdot 7 = 14

Отсюда радиус равен \frac{d}{2}=7