Задание №314
Условие
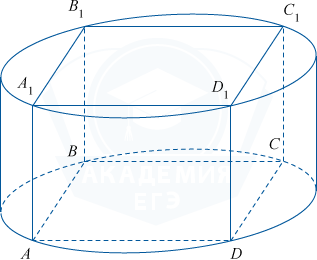
Основанием прямой призмы является квадрат, сторона которого равна 4. Длина бокового ребра призмы равна \frac{8}{\pi}. Найдите объем цилиндра, описанного около этой призмы.
Решение
Радиус окружности, описанной вокруг квадрата со стороной 4, равен r=\frac{4}{\sqrt2}=2\sqrt2.
Объем цилиндра равен V= \pi r^2h= \pi\cdot(2\sqrt2)^2\cdot\frac{8}{\pi}= \pi\cdot8\cdot\frac{8}{\pi}= 64.
Ответ
64
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.