Задание №113
Условие
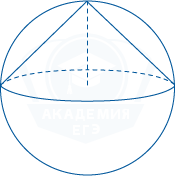
Около конуса с образующей равной 7\sqrt{2} описана сфера. Сфера содержит вершину конуса и его основание. Центр основания конуса и центр сферы совпадают. Найдите радиус сферы.
Решение
Так как центры сферы и основания конуса совпадают, то образующие конуса пересекаются под прямым углом. Найдем гипотенузу прямоугольного треугольника, катетами которого являются образующие конуса, а гипотенузой – диаметр сферы. Воспользуемся теоремой Пифагора:
d^2=2\cdot (7\sqrt{2})^2=2\cdot 2\cdot 7^2=2^2\cdot 7^2
d = 2\cdot 7 = 14
Отсюда радиус равен \frac{d}{2}=7