Задания по теме «Геометрические фигуры в пространстве: нахождение длины, площади, объема»

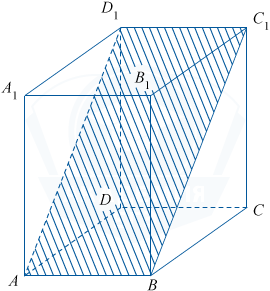
Прямая AB параллельна плоскости DD_1C_1C. Тогда плоскость, проходящая через неё, пересекает плоскость DD_1C_1C по прямой, параллельной AB. Такой прямой будет прямая D_1C_1. Значит, в сечении получается параллелограмм ABC_1D_1.

Так как AB\perp BB_1C_1C, то AB\perp BC_1, поэтому параллелограмм ABC_1D_1 является прямоугольником. S_{ABC_1D_1} =AB\cdot BC_1. Найдем BC_1 по теореме Пифагора: BC_1^2 = BC^2 + CC_1^2 = 6^2 + 8^2 = 36 + 64 = 100, BC_1 = 10. Отсюда,

S_{ABC_1D_1} = AB \cdot BC_1 = 4 \cdot 10 = 40.

Ребро D_2D перпендикулярно плоскости ABCD, поэтому угол D_2DB — прямой. Тогда tg \angle D_2BD =\frac{D_2D}{DB}. По теореме Пифагора (DB)^2 = (AD)^2 + (AB)^2 = 16 + 16 = 32. DB = 4\sqrt2. Отсюда, tg \angle D_2BD =\frac{4}{4\sqrt2}=\frac{1}{\sqrt2}, (tg\angle D_2BD)^2=\frac12=0,5.

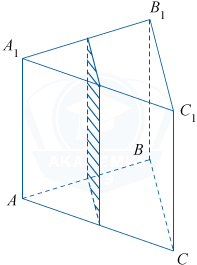
Рассмотрим следующий рисунок.

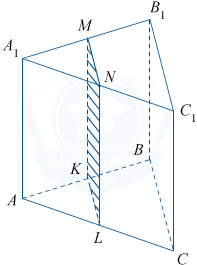
Отрезок MN является средней линией треугольника A_1B_1C_1, поэтому MN = \frac12 B_1C_1=2. Аналогично, KL=\frac12BC=2. Кроме того, MK = NL = 10. Отсюда следует, что четырёхугольник MNLK является параллелограммом. Так как MK\parallel AA_1, то MK\perp ABC и MK\perp KL. Следовательно, четырёхугольник MNLK является прямоугольником. S_{MNLK} = MK\cdot KL = 10\cdot 2 = 20.

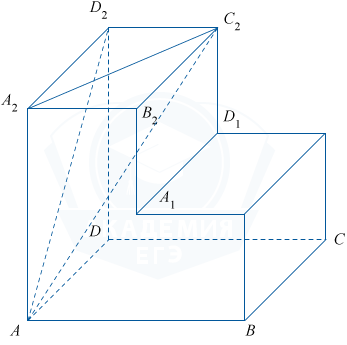
Ребро C_2D_2 перпендикулярно плоскости AA_2D_2D, поэтому угол C_2D_2A — прямой. По теореме Пифагора (AC_2)^2 =  (AD_2)^2 +(D_2C_2)^2. (AD_2)^2 =  (AD)^2 +(DD_2)^2 =  4^2 + 4^2 =  32. Отсюда, (AC_2)^2 = 32 + 2^2 = 36,  AC_2 = 6.

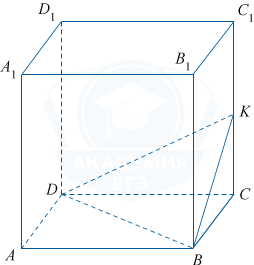
Согласно условию, KC является высотой пирамиды KBCD. CC_1 является высотой призмы ABCDA_1B_1C_1D_1.

Так как K является серединой CC_1, то KC=\frac12CC_1. Пусть CC_1=H, тогдаKC=\frac12H. Заметим также, что S_{BCD}=\frac12S_{ABCD}. Тогда, V_{KBCD}= \frac13S_{BCD}\cdot\frac{H}{2}= \frac13\cdot\frac12S_{ABCD}\cdot\frac{H}{2}= \frac{1}{12}\cdot S_{ABCD}\cdot H= \frac{1}{12}V_{ABCDA_1B_1C_1D_1}. Следовательно, V_{KBCD}=\frac{1}{12}\cdot24=2.

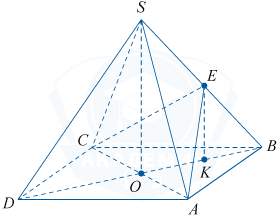
На рисунке SO является высотой пирамиды ABCD, EK является перпендикуляром к плоскости ABCD (значит, EK является высотой пирамиды EABC), поэтому

EK\parallel SO и SO и EK лежат в одной плоскости SOB.

Так как E является серединой SB, то EK является средней линией треугольника SOB, значит, EK = \frac12SO. Пусть SO = H, тогда EK = \frac12 H. Заметим также, что S_{ABC} = \frac12 S_{ABCD}. Тогда V_{EABC}= \frac13 S_{ABC}\cdot\frac{H}{2}= \frac13\cdot\frac12 S_{ABCD}\cdot\frac{H}{2}= \frac14\cdot\frac13 S_{ABCD}\cdot H= \frac14 V_{SABCD}. Следовательно, V_{EABC}=\frac14\cdot16=4.

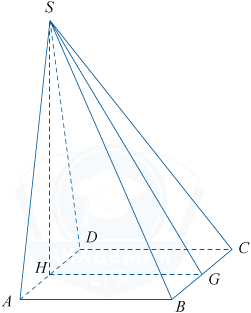
Объём пирамиды вычисляется по формуле V = \frac13\cdot S_осн.· h, где S_осн. — площадь основания, а h — высота пирамиды, равная 9. На рисунке, приведённом в условии задачи, SH — высота пирамиды и HG\perp BC. Покажем, что угол SAH является линейным углом двугранного угла между плоскостью ABS и плоскостью основания ABC, которые пересекаются по прямой AB. AH\perp AB, так как основание призмы является прямоугольником. AH является проекцией наклонной AS. Тогда по теореме о трех перпендикулярах AS\perp AB. Отсюда \frac{SH}{AH}=tg60^{\circ}=\sqrt3. \frac{9}{AH}=\sqrt3, AH=\frac{9}{\sqrt3}=3\sqrt3, AD=2AH=6\sqrt3. Аналогично убеждаемся, что угол SGH равен 60^{\circ} и HG=3\sqrt3=BC. Следовательно стороны прямоугольника, лежащего в основании, равны 3\sqrt3 и 6\sqrt3. Значит V=\frac13\cdot S_осн. · h = \frac13\cdot3\sqrt3\cdot6\sqrt3\cdot9= 162.

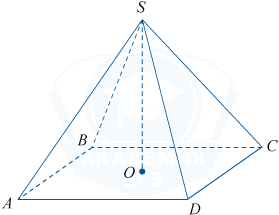
Объём пирамиды вычисляется по формуле V=\frac13\cdot S_{osn.} \cdot h, где S_{osn} — площадь основания, а h — высота пирамиды. Отсюда h = \frac{3V}{S_{osn.}}. Площадь основания является площадью прямоугольника со сторонами 6 и 8, поэтому S_{osn.} = 6 \cdot 8 = 48. Отсюда h = \frac{3\cdot64}{48}=4.

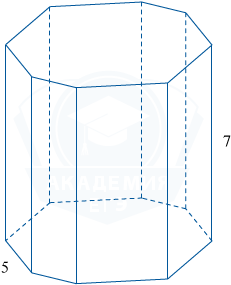
Площадь боковой поверхности призмы находим по формуле S_бок. = P_осн. · h = 8a\cdot h, где P_осн. и h — соответственно периметр основания и высота призмы, равная 7, и a — сторона правильного восьмиугольника, равная 5. Следовательно, S_бок. = 8\cdot 5\cdot 7 = 280.

Площадь боковой поверхности призмы находим по формуле S_бок. = P_осн. · h = 6a\cdot h, где P_осн. и h — соответственно периметр основания и высота призмы, равная 8, и a — сторона правильного шестиугольника, равная 6. Следовательно, S_бок. = 6\cdot 6\cdot 8 = 288.