Задания по теме «Пирамида»

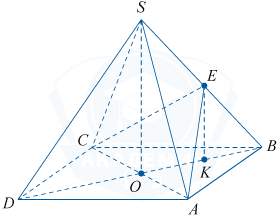
На рисунке SO является высотой пирамиды ABCD, EK является перпендикуляром к плоскости ABCD (значит, EK является высотой пирамиды EABC), поэтому

EK\parallel SO и SO и EK лежат в одной плоскости SOB.

Так как E является серединой SB, то EK является средней линией треугольника SOB, значит, EK = \frac12SO. Пусть SO = H, тогда EK = \frac12 H. Заметим также, что S_{ABC} = \frac12 S_{ABCD}. Тогда V_{EABC}= \frac13 S_{ABC}\cdot\frac{H}{2}= \frac13\cdot\frac12 S_{ABCD}\cdot\frac{H}{2}= \frac14\cdot\frac13 S_{ABCD}\cdot H= \frac14 V_{SABCD}. Следовательно, V_{EABC}=\frac14\cdot16=4.

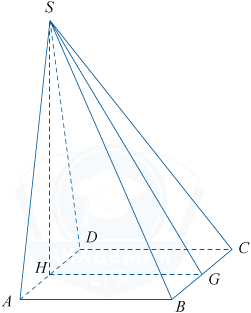
Объём пирамиды вычисляется по формуле V = \frac13\cdot S_осн.· h, где S_осн. — площадь основания, а h — высота пирамиды, равная 9. На рисунке, приведённом в условии задачи, SH — высота пирамиды и HG\perp BC. Покажем, что угол SAH является линейным углом двугранного угла между плоскостью ABS и плоскостью основания ABC, которые пересекаются по прямой AB. AH\perp AB, так как основание призмы является прямоугольником. AH является проекцией наклонной AS. Тогда по теореме о трех перпендикулярах AS\perp AB. Отсюда \frac{SH}{AH}=tg60^{\circ}=\sqrt3. \frac{9}{AH}=\sqrt3, AH=\frac{9}{\sqrt3}=3\sqrt3, AD=2AH=6\sqrt3. Аналогично убеждаемся, что угол SGH равен 60^{\circ} и HG=3\sqrt3=BC. Следовательно стороны прямоугольника, лежащего в основании, равны 3\sqrt3 и 6\sqrt3. Значит V=\frac13\cdot S_осн. · h = \frac13\cdot3\sqrt3\cdot6\sqrt3\cdot9= 162.

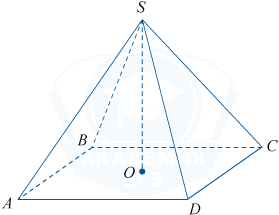
Объём пирамиды вычисляется по формуле V=\frac13\cdot S_{osn.} \cdot h, где S_{osn} — площадь основания, а h — высота пирамиды. Отсюда h = \frac{3V}{S_{osn.}}. Площадь основания является площадью прямоугольника со сторонами 6 и 8, поэтому S_{osn.} = 6 \cdot 8 = 48. Отсюда h = \frac{3\cdot64}{48}=4.

Объем пирамиды вычисляется по формуле

V=\frac13Sh

где S – площадь основания; h – высота пирамиды

Для нахождения площади, найдем диагональ квадрата основания пирамиды. Рассмотрим прямоугольный треугольник, гипотенузой которого является сторона пирамиды, а одним из катетов высота пирамиды. По теореме Пифагора диагональ будет равна:

d=2\cdot\sqrt{4^2-2^2}=2\cdot\sqrt{12}=4\sqrt{3}

Зная угол CAB = 45^{\circ} прямоугольного треугольника ABC мы можем найти сторону AB:

AB=d\cdot\cos 45^{\circ}=4\sqrt{3}\cdot \frac{1}{\sqrt{2}}=4\sqrt{3}\cdot \frac{\sqrt{2}}{2}=2\sqrt{6}

Площадь основания равна:

S = \left ( 2\sqrt{6} \right )^2=4\cdot 6=24

Объем пирамиды равен:

V = \frac13\cdot 24\cdot 2=16

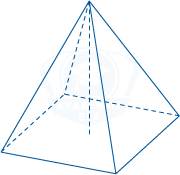
Основанием правильной четырехугольной пирамиды является квадрат. По теореме Пифагора найдем диагональ квадрата, центр которой пересекает вершина пирамиды.

d^2=10^2+10^2=200

d=10\sqrt{2}

Рассмотрим прямоугольный треугольник, в котором один катет является половиной диагонали квадрата основания пирамиды, а гипотенуза равна ее боковому ребру. По теореме Пифагора найдем второй катет, являющийся высотой пирамиды:

h^2=(7,5)^2-\left ( \frac{10\sqrt{2}}{2} \right )^2=56,25-50=6,25

h = \sqrt{6,25} = 2,5