Открытый банк заданий по теме производная и первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)
Прямая y=3x+2 является касательной к графику функции y=-12x^2+bx-10. Найдите b, учитывая, что абсцисса точки касания меньше нуля.
Пусть x_0 — абсцисса точки на графике функции y=-12x^2+bx-10, через которую проходит касательная к этому графику.
Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=-24x_0+b=3. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть -12x_0^2+bx_0-10=3x_0+2. Получаем систему уравнений \begin{cases} -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \end{cases}
Решая эту систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания меньше нуля, поэтому x_0=-1, тогда b=3+24x_0=-21.
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).
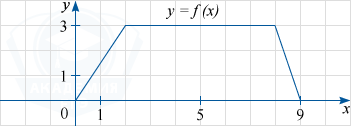
По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.
Её площадь равна \frac{4+3}{2}\cdot 3=10,5.
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-4; 10). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
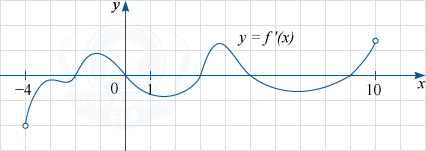
Как известно, функция f(x) убывает на тех промежутках, в каждой точке которых производная f'(x) меньше нуля. Учитывая, что надо находить длину наибольшего из них естественно по рисунку выделяются три таких промежутка: (-4; -2); (0; 3); (5; 9).
Длина наибольшего из них — (5; 9) равна 4.
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-8; 7). Найдите количество точек максимума функции f(x), принадлежащих промежутку [-6; -2].
.png)
Из графика видно, что производная f'(x) функции f(x) меняет знак с плюса на минус (именно в таких точках будет максимум) ровно в одной точке (между -5 и -4) из промежутка [-6; -2]. Поэтому на промежутке [-6; -2] ровно одна точка максимума.
На рисунке изображён график функции y=f(x), определённой на интервале (-2; 8). Определите количество точек, в которых производная функции f(x) равна 0.
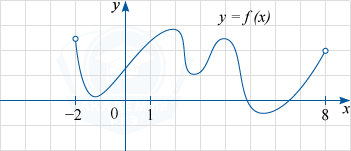
Равенство нулю производной в точке означает, что касательная к графику функции, проведённая в этой точке, параллельна оси Ox. Поэтому находим такие точки, в которых касательная к графику функции параллельна оси Ox. На данном графике такими точками являются точки экстремума (точки максимума или минимума). Как видим, точек экстремума 5.
Прямая y=-3x+4 параллельна касательной к графику функции y=-x^2+5x-7. Найдите абсциссу точки касания.
Угловой коэффициент прямой к графику функции y=-x^2+5x-7 в произвольной точке x_0 равен y'(x_0). Но y'=-2x+5, значит, y'(x_0)=-2x_0+5. Угловой коэффициент прямой y=-3x+4, указанной в условии, равен -3. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что =-2x_0 +5=-3.
Получаем: x_0 = 4.
На рисунке изображён график функции y=f(x) и отмечены точки -6, -1, 1, 4 на оси абсцисс. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
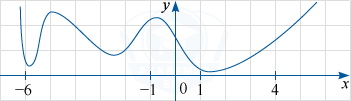
Проводим касательные к графику функции в точках с указанными абсциссами. Определяем, под каким углом они наклонены к положительному направлению оси Ox. Как известно, значение тангенса указанного угла это и есть значение производной в указанных точках.
В точках -1 и 4 касательные наклонены под острым углом, поэтому в этих точках значение производной отрицательно. Учитывая, что в точке x=-6 касательная наклонена под меньшим тупым углом (ближе к вертикальной прямой), значение производной в этой точке наименьшее.
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].
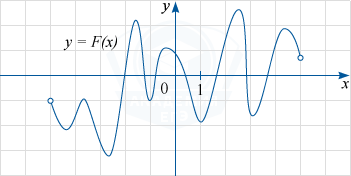
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.
.png)
По рисунку определяем, что касательная проходит через точки A(-6; 2) и B(-1; 1). Обозначим через C(-6; 1) точку пересечения прямых x=-6 и y=1, а через \alpha угол ABC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол \pi -\alpha, который является тупым.
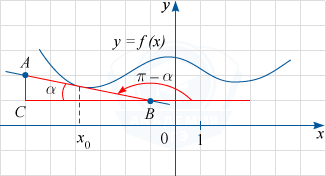
Как известно, tg(\pi -\alpha) и будет значением производной функции f(x) в точке x_0. Заметим, что tg \alpha =\frac{AC}{CB}=\frac{2-1}{-1-(-6)}=\frac15. Отсюда по формулам приведения получаем: tg(\pi -\alpha ) =-tg \alpha =-\frac15=-0,2.
Прямая y=-2x-4 является касательной к графику функции y=16x^2+bx+12. Найдите b, учитывая, что абсцисса точки касания больше нуля.
Пусть x_0 — абсцисса точки на графике функции y=16x^2+bx+12, через которую
проходит касательная к этому графику.
Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=32x_0+b=-2. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть 16x_0^2+bx_0+12=-2x_0-4. Получаем систему уравнений \begin{cases} 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4. \end{cases}
Решая систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания больше нуля, поэтому x_0=1, тогда b=-2-32x_0=-34.
Закажите обратный звонок!