Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).
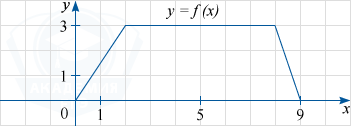
По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.
Её площадь равна \frac{4+3}{2}\cdot 3=10,5.
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].
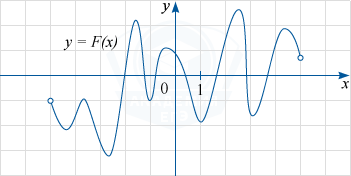
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).
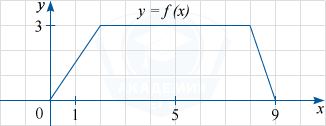
По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.
Её площадь равна \frac{5+3}{2}\cdot 3=12.
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].
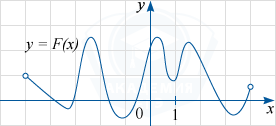
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 3], в которых производная функции F(x) равна нулю.
Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).
Найдите площадь заштрихованной фигуры.
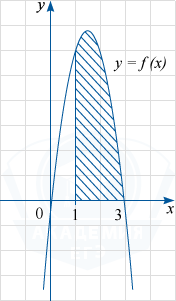
Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)\cdot 3^2 -7-(-1^3 +(4,5)\cdot 1^2 -7)= 6,5-(-3,5)= 10.
На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
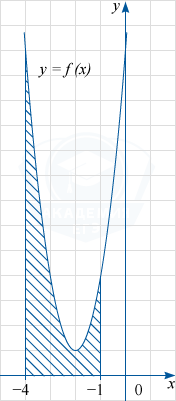
Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).
Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-\frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
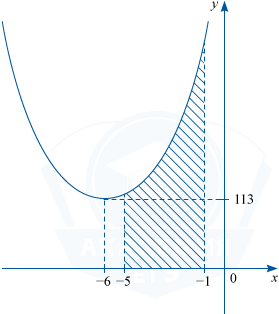
По формуле Ньютона-Лейбница S=F(-1)-F(-5).
F(-1)= (-1)^3+18\cdot(-1)^2+221\cdot(-1)-\frac12= -204-\frac12.
F(-5)= (-5)^3+18\cdot(-5)^2+221\cdot(-5)-\frac12= -125+450-1105-\frac12= -780-\frac12.
F(-1)-F(-5)= -204-\frac12-\left (-780-\frac12\right)= 576.
На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).
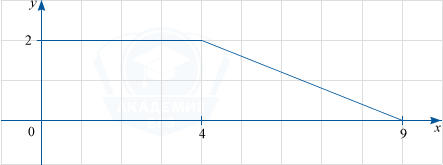
F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,\:x=9. Рассмотрим рисунок ниже.
Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна \frac{6+1}{2}\cdot2=7.
На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-\frac13x^3-\frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.
.png)
На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:
\int\limits_{-4}^{-1}f(x)dx=F(-1)-F(-4)
Подставим значение первообразной из условия и получим площадь фигуры:
F(-1)-F(-4)=
=\frac13-\frac52+4+2-\frac{64}{3}+\frac{80}{2}-16-2=
=-\frac{63}{3}+\frac{75}{2}-12=-21+37,5-12=4,5
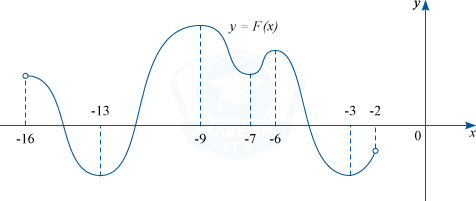
Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].
Формула первообразной имеет следующий вид:
f(x) = F'(x)
По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.
Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.
На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.
.png)
Закажите обратный звонок!