Задание №907
Условие
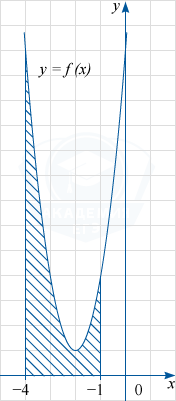
На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
Решение
Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).
Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Михаил Тушин /