Задания по теме «Геометрический смысл производной. Касательная к графику функции»

Пусть x_0 — абсцисса точки на графике функции y=-12x^2+bx-10, через которую проходит касательная к этому графику.

Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=-24x_0+b=3. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть -12x_0^2+bx_0-10=3x_0+2. Получаем систему уравнений \begin{cases} -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \end{cases}

Решая эту систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания меньше нуля, поэтому x_0=-1, тогда b=3+24x_0=-21.

Угловой коэффициент прямой к графику функции y=-x^2+5x-7 в произвольной точке x_0 равен y'(x_0). Но y'=-2x+5, значит, y'(x_0)=-2x_0+5. Угловой коэффициент прямой y=-3x+4, указанной в условии, равен -3. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что =-2x_0 +5=-3.

Получаем: x_0 = 4.

По рисунку определяем, что касательная проходит через точки A(-6; 2) и B(-1; 1). Обозначим через C(-6; 1) точку пересечения прямых x=-6 и y=1, а через \alpha угол ABC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол \pi -\alpha, который является тупым.

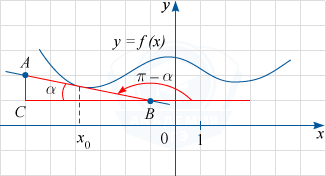
Как известно, tg(\pi -\alpha) и будет значением производной функции f(x) в точке x_0. Заметим, что tg \alpha =\frac{AC}{CB}=\frac{2-1}{-1-(-6)}=\frac15. Отсюда по формулам приведения получаем: tg(\pi -\alpha ) =-tg \alpha =-\frac15=-0,2.

Пусть x_0 — абсцисса точки на графике функции y=16x^2+bx+12, через которую

проходит касательная к этому графику.

Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=32x_0+b=-2. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть 16x_0^2+bx_0+12=-2x_0-4. Получаем систему уравнений \begin{cases} 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4. \end{cases}

Решая систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания больше нуля, поэтому x_0=1, тогда b=-2-32x_0=-34.

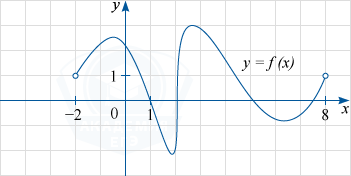
Прямая y=6 параллельна оси Ox. Поэтому находим такие точки, в которых касательная к графику функции параллельна оси Ox. На данном графике такими точками являются точки экстремума (точки максимума или минимума). Как видим, точек экстремума 4.

Угловой коэффициент касательной к графику функции y=x^2-4x+9 в произвольной точке x_0 равен y'(x_0). Но y'=2x-4, значит, y'(x_0)=2x_0-4. Угловой коэффициент касательной y=4x-7, указанной в условии, равен 4. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что 2x_0-4=4. Получаем: x_0=4.

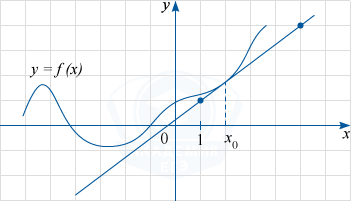
По рисунку определяем, что касательная проходит через точки A(1; 1) и B(5; 4). Обозначим через C(5; 1) точку пересечения прямых x=5 и y=1, а через \alpha угол BAC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол \alpha.

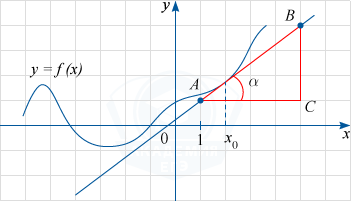
Как известно, tg \alpha и будет значением производной функции f(x) в точке x_0.

Заметим, что tg \alpha =\frac{BC}{AC}=\frac34=0,75.

Угловой коэффициент касательной к графику функции y=x^3+3x^2-11x-3 в произвольной точке x_0 равен y'(x_0). Но y'=3x^2+6x-11, значит y'(x_0)=3x_0^2+6x_0-11. Угловой коэффициент касательной y=-2x-8, указанной в условии равен -2. Поэтому находим такое значение x_0, что 3x_0^2+6x_0-11=-2,  3x_0^2+6x_0-9=0. По формулам корней квадратного уравнения получаем, что либо x_0=-3, либо x_0=1.

Заметим, что y(-3)= (-3)^3+3\cdot (-3)^2-11\cdot (-3)-3= 30, а y(1)= 1^3+3\cdot 1^2-11\cdot 1-3= -10. Получаем две возможные точки касания: (-3; 30); (1; -10). Выясним, через какую из них проходит касательная y=2x-8. Координаты точки (-3; 30) не удовлетворяют уравнению касательной, так как равенство 30=-2\cdot (-3)-8 не является верным. Но равенство -10=(-2)\cdot 1-8 является верным. Поэтому касательная проходит через точку (1, -10) с абсциссой, равной 1.

Пусть (x_0; y_0) — точка, в которой прямая y=-2x+5 касается графика функции y=ax^2+2x+7. Тогда угловой коэффициент касательной к графику функции y=ax^2+2x+7 в точке x_0 равен y'(x_0). Но y'=2ax+2, значит y'(x_0)=2ax_0+2.

Угловой коэффициент касательной y=-2x+5, указанной в условии, равен -2. Поэтому 2ax_0+2=-2. Отсюда, a \neq 0.

Кроме того точка (x_0; y_0) лежит на прямой y=-2x+5 и на графике функции y=ax^2+2x+7. Значит, выполняется равенство y_0=-2x_0+5=ax_0^2+2x_0+7. Получаем систему:

\begin{cases} 2ax_0+2=-2, \\ -2x_0+5=ax_0^2+2x_0+7; \end{cases}

\begin{cases} x_0=-\frac2a, \\ ax_0^2+4x_0+2=0; \end{cases}

a\left(-\frac2a\right)^2+4\left(-\frac2a\right)+2=0,

\frac4a-\frac8a+2=0,

\frac4a=2,

a=2;

Пусть x_0 — абсцисса точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней. Тогда значение производной y=f'(x) в точке x_0 равно 0, так как угловой коэффициент оси абсцисс y=0 равен 0.

Но из графика видно, что f'(x)=0 в единственной точке x_0=-5.

Действительно, прямая y=0 пересекает график функции y=f'(x) в единственной точке (-5; 0), абсцисса которой равна -5.