Задание №1086
Условие
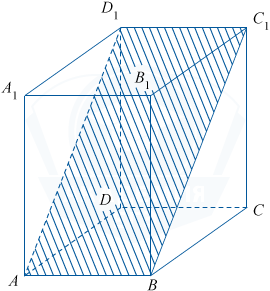
В прямоугольном параллелепипеде ABCDA_1B_1C_1D_1 известны длины рёбер: AB = 4, BC = 6, AA_1 = 8. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C_1.
Решение
Прямая AB параллельна плоскости DD_1C_1C. Тогда плоскость, проходящая через неё, пересекает плоскость DD_1C_1C по прямой, параллельной AB. Такой прямой будет прямая D_1C_1. Значит, в сечении получается параллелограмм ABC_1D_1.
Так как AB\perp BB_1C_1C, то AB\perp BC_1, поэтому параллелограмм ABC_1D_1 является прямоугольником. S_{ABC_1D_1} =AB\cdot BC_1. Найдем BC_1 по теореме Пифагора: BC_1^2 = BC^2 + CC_1^2 = 6^2 + 8^2 = 36 + 64 = 100, BC_1 = 10. Отсюда,
S_{ABC_1D_1} = AB \cdot BC_1 = 4 \cdot 10 = 40.
Ответ
40
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.