Задания по теме «Параллелепипед»
Открытый банк заданий по теме параллелепипед. Задания B8 из ЕГЭ по математике (профильный уровень)
Открытый банк заданий по теме параллелепипед. Задания B8 из ЕГЭ по математике (профильный уровень)
В прямоугольном параллелепипеде ABCDA_1B_1C_1D_1 известны длины рёбер: AB = 4, BC = 6, AA_1 = 8. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C_1.
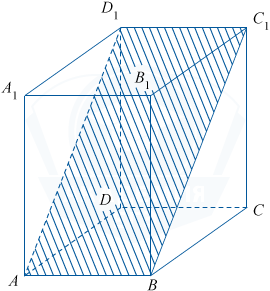
Прямая AB параллельна плоскости DD_1C_1C. Тогда плоскость, проходящая через неё, пересекает плоскость DD_1C_1C по прямой, параллельной AB. Такой прямой будет прямая D_1C_1. Значит, в сечении получается параллелограмм ABC_1D_1.
Так как AB\perp BB_1C_1C, то AB\perp BC_1, поэтому параллелограмм ABC_1D_1 является прямоугольником. S_{ABC_1D_1} =AB\cdot BC_1. Найдем BC_1 по теореме Пифагора: BC_1^2 = BC^2 + CC_1^2 = 6^2 + 8^2 = 36 + 64 = 100, BC_1 = 10. Отсюда,
S_{ABC_1D_1} = AB \cdot BC_1 = 4 \cdot 10 = 40.
Гранью параллелепипеда является ромб со стороной 2 и острым углом 60^{\circ}. Одно из рёбер параллелепипеда составляет с плоскостью этой грани угол 60^{\circ} и равно 4. Найдите объём параллелепипеда.
Примем указанную в условии грань параллелепипеда за его основание. Тогда параллелепипед будет наклонной призмой, объём V которой находим по формуле V = Sосн. · h, где Sосн. — площадь основания, а h — высота призмы. Опустим из точки A_1 верхнего основания перпендикуляр A_1K на нижнее основание.
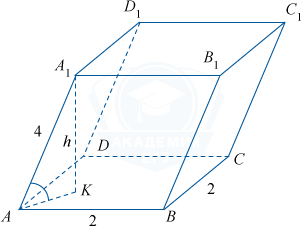
Тогда A_1K будет высотой призмы, A_1K=h. \angle A_1AK является углом между ребром AA_1 и плоскостью основания, по условию он равен 60^{\circ}. Тогда A_1K= AA_1\cdot\sin60^{\circ}= 4\cdot\frac{\sqrt3}{2}= 2\sqrt3.
Площадь основания, являющегося ромбом, находим по формуле Sосн. = AB\cdot AD\cdot\sin60^{\circ}= 2\cdot2\cdot\frac{\sqrt3}{2}= 2\sqrt3.
Отсюда, V = Sосн. · h = 2\sqrt3\cdot2\sqrt3=12.
Прямоугольный параллелепипед имеет следующие длины ребер AB=7, AD=24, AA_1=18. Найдите синус угла между прямыми CD и A_1C_1.
Рассмотрим рисунок:
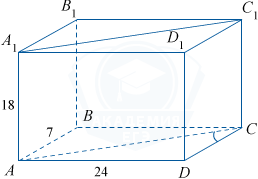
Угол между прямыми DC и A_1C_1 совпадает с углом между прямыми DC и AC, так как AC \parallel A_1C_1.
\sin\angle ACD= \frac{AD}{AC}= \frac{24}{\sqrt{24^2+7^2}}= \frac{24}{\sqrt{625}}= \frac{24}{25}= 0,96.
Параллелепипед ABCDA_1B_1C_1D_1 имеет объем, равный 4,8 м3. Определите объем треугольной пирамиды, которая образована вершинами ACB_1D_1
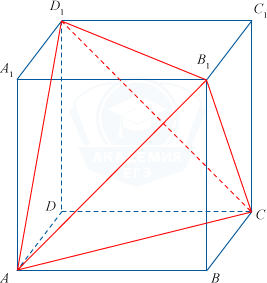
.png) Треугольная пирамида разбила свободное пространство параллелепипеда на 4 равных прямоугольных пирамиды. Для того, чтобы найти объем пирамиды ACB_1D_1, необходимо из объема параллелепипеда вычесть объем свободной области (т.е. 4·объем каждой из маленьких прямоугольных пирамид).
Треугольная пирамида разбила свободное пространство параллелепипеда на 4 равных прямоугольных пирамиды. Для того, чтобы найти объем пирамиды ACB_1D_1, необходимо из объема параллелепипеда вычесть объем свободной области (т.е. 4·объем каждой из маленьких прямоугольных пирамид).
Объем параллелепипеда равен произведению длин его сторон:
V = AB \cdot BC \cdot BB_1
Объем выделенной пирамиды Vпир определяется как произведение \frac13 площади основания на высоту:
Vпир = \frac13 \cdot S_{ABC} \cdot BB_1
S_{ABC} = \frac12 AB \cdot BC
Vпир = \frac13 \cdot\frac12 AB \cdot BC\cdot BB_1 = \frac{AB \cdot BC \cdot BB_1}{6} = \frac{V}{6}
Найдем объем пирамиды, образованной вершинами ACB_1D_1. Для этого вычтем из объема параллелепипеда объемы четырех пирамид, которые занимают свободное пространство (они равны друг другу):
Vтреуг = V – 4·Vпир = V-4 \cdot \frac{V}{6} = \frac13V
Подставляя значение V = 4,8 м3, получили:
Vтреуг = \frac{4,8}{3}=1,6 м3
Закажите обратный звонок!