Задание №86
Условие
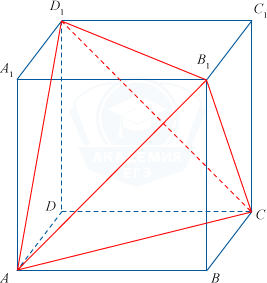
Параллелепипед ABCDA_1B_1C_1D_1 имеет объем, равный 4,8 м3. Определите объем треугольной пирамиды, которая образована вершинами ACB_1D_1
Решение
.png) Треугольная пирамида разбила свободное пространство параллелепипеда на 4 равных прямоугольных пирамиды. Для того, чтобы найти объем пирамиды ACB_1D_1, необходимо из объема параллелепипеда вычесть объем свободной области (т.е. 4·объем каждой из маленьких прямоугольных пирамид).
Треугольная пирамида разбила свободное пространство параллелепипеда на 4 равных прямоугольных пирамиды. Для того, чтобы найти объем пирамиды ACB_1D_1, необходимо из объема параллелепипеда вычесть объем свободной области (т.е. 4·объем каждой из маленьких прямоугольных пирамид).
Объем параллелепипеда равен произведению длин его сторон:
V = AB \cdot BC \cdot BB_1
Объем выделенной пирамиды Vпир определяется как произведение \frac13 площади основания на высоту:
Vпир = \frac13 \cdot S_{ABC} \cdot BB_1
S_{ABC} = \frac12 AB \cdot BC
Vпир = \frac13 \cdot\frac12 AB \cdot BC\cdot BB_1 = \frac{AB \cdot BC \cdot BB_1}{6} = \frac{V}{6}
Найдем объем пирамиды, образованной вершинами ACB_1D_1. Для этого вычтем из объема параллелепипеда объемы четырех пирамид, которые занимают свободное пространство (они равны друг другу):
Vтреуг = V – 4·Vпир = V-4 \cdot \frac{V}{6} = \frac13V
Подставляя значение V = 4,8 м3, получили:
Vтреуг = \frac{4,8}{3}=1,6 м3