Задание №317
Условие
Прямоугольный параллелепипед имеет следующие длины ребер AB=7, AD=24, AA_1=18. Найдите синус угла между прямыми CD и A_1C_1.
Решение
Рассмотрим рисунок:
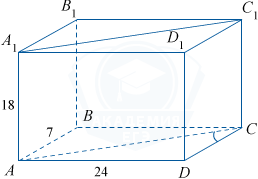
Угол между прямыми DC и A_1C_1 совпадает с углом между прямыми DC и AC, так как AC \parallel A_1C_1.
\sin\angle ACD= \frac{AD}{AC}= \frac{24}{\sqrt{24^2+7^2}}= \frac{24}{\sqrt{625}}= \frac{24}{25}= 0,96.
Ответ
0,96
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.