Задание №1082
Условие
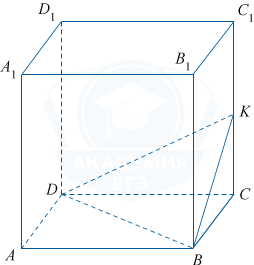
Объём правильной четырёхугольной призмы ABCDA_1B_1C_1D_1 равен 24. Точка K — середина ребра CC_1. Найдите объём пирамиды KBCD.
Решение
Согласно условию, KC является высотой пирамиды KBCD. CC_1 является высотой призмы ABCDA_1B_1C_1D_1.
Так как K является серединой CC_1, то KC=\frac12CC_1. Пусть CC_1=H, тогдаKC=\frac12H. Заметим также, что S_{BCD}=\frac12S_{ABCD}. Тогда, V_{KBCD}= \frac13S_{BCD}\cdot\frac{H}{2}= \frac13\cdot\frac12S_{ABCD}\cdot\frac{H}{2}= \frac{1}{12}\cdot S_{ABCD}\cdot H= \frac{1}{12}V_{ABCDA_1B_1C_1D_1}. Следовательно, V_{KBCD}=\frac{1}{12}\cdot24=2.